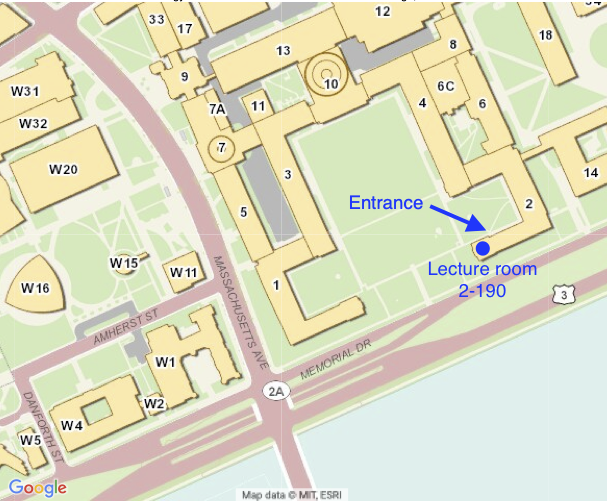
The talks are in the room 2-190. Some or all building entrance doors on MIT campus will be locked. We suggest the participants enter through the door next to the lecture room
in the Building 2 courtyard. We originally asked for this door to remain unlocked during the conference, but due to the protests at MIT all the doors will be locked on Friday and the situation is unclear for Saturday and Sunday. Please see the map below:
Each talk is 60 minutes long.
The conference dinner is in the Mathematics Common Room, 2-290. It is limited to the participants who have signed up for it via the second registration form. No lunch is provided but there are many lunch places within a 10 minute walk from Building 2.
-
Xuwen Zhu (Northeastern University)
Analysis and degeneration of gravitational instantons
[ Slides ]
Gravitational instantons are non-compact Calabi–Yau metrics with $L^2$ bounded curvature and are categorized into six types. We will focus on one such type, called ALH* metrics, which has a non-compact end with inhomogeneous collapsing near infinity. Such metrics appeared recently in the works on the SYZ conjecture, as well as the scaling bubble limits for codimension-3 collapsing of K3 surfaces. I will talk about a joint project with Rafe Mazzeo on the Fredholm mapping property and $L^2$ cohomology of ALH* metrics, where the geometric microlocal analysis of fibered metrics plays a central role. I will also discuss the joint work with Yu-Shen Lin and Sidharth Soundararajan on the degeneration of such metrics which gives a partial compactification of their moduli space.
-
Michael Hopkins (Harvard University)
Algebraic vector bundles on smooth affine varieties
In the 1970s Griffiths outlined a program to use a generalization of value distribution theory to study the obstructions to finding algebraic structures on holomorphic vector bundles over affine complex varieties. In this talk I will describe joint work with Aravind Asok and Tom Bachmann that shows that some of the ideas envisioned by Griffiths work out to be stronger than originally envisioned.
-
András Vasy (Stanford University)
Microlocal analysis near null infinity on asymptotically flat spacetimes
[ Slides ]
There are a number of reasons due to which it is advantageous to have a phase space based, or microlocal, approach available for analyzing wave propagation. In this talk I will explain a microlocal framework for wave propagation on asymptotically flat spacetimes of arbitrary dimension which in particular includes operator corresponding to Lorentzian metrics arising from solutions of Einstein's equations in the 4 spacetime dimensional setting. On the compactification of Minkowski space that underlies this, which is a manifold with corners (with the usual null infinity, scri, being a boundary hypersurface), the operators lie in a combination of Melrose's totally characteristic (also called b), and Mazzeo's edge pseudodifferential operator algebras. I will give an introduction via a simpler setting (which includes Minkowski space and a different class of perturbations), and then explain the reasons for, and complications with, moving to the present setting. Along the way, I will also briefly describe the related Klein–Gordon work of Ethan Sussman. This is joint work with Peter Hintz.
-
Rafe Mazzeo (Stanford University)
Bringing coals to Newcastle: a report on $\mathbb Z_2$ harmonic spinors
This talk will be partly historical, with thoughts on Melrose's ideas which led to the development of geometric microlocal analysis, together with a report on some recent and not so recent results by various people concerning the existence and nature of $\mathbb Z_2$ harmonic spinors and 1-forms, as initiated by Taubes. These two parts of the talk are closely related.
-
Sun-Yung Alice Chang (Princeton University)
On a conformal Einstein fill in problem
[ Slides ]
Given a manifold $(M^n,h)$, when is it the boundary of a conformally compact Einstein manifold $(X^{n+1},g)$, in the sense that there exists some defining function $r$ on $X$ so that $r^2 g$ is compact on the closure of $X$ and $r^2 g$ restricted to $M$ is the given metric $h$? The model example is the $n$-sphere as the conformal infinity of the hyperbolic $(n+1)$-ball.
In the special case when $n = 3$, one can formulate the problem as a Dirichlet to Neumann type inverse problem. In the talk, I will report on some progress made with Yuxin Ge on the issues of the `compactness', and as an application, the `existence' and `uniqueness' of the fill in problem for a class of metrics of positive scalar curvature defined on the 3-sphere.
-
Dan Freed (Harvard University)
Index theory on pin manifolds
[ Slides ]
Though index theory on pin manifolds has appeared sporadically, there is not
a systematic theory. A few recent projects with Mike Hopkins led us to a
more unified perspective. I will explain these ideas in the general context
of topological and geometric index theory.
-
Peter Sarnak (Princeton University)
The arithmetic structure of the spectrum of a metric graph
[ Slides ]
Endowing a finite combinatorial graph with lengths on its edges defines singular 1-dimensional Riemannian manifolds known as metric graphs. The spectra of their Laplacians have been widely studied. We show that these spectra have a structured linear part described in terms of arithmetic progressions and a nonlinear `random' part which is highly linearly and even algebraically independent over the rationals. These spectra give rise to exotic crystalline measures (`Generalised Poisson Summation Formulae') and resolve various open problems concerning the latter. Joint work with Pavel Kurasov.
-
Gunther Uhlmann (University of Washington)
Microlocal Analysis and Inverse Problems
[ Slides ]
We consider two geometric inverse problems. The first is to
recover a Riemannian metric of a compact Riemannian manifold with
boundary from the distance function between boundary points. This
problem arises in global seismology in attempting to determine the
inner structure of the Earth from travel times of earthquakes. The
other is to recover the metric of a Lorentzian manifold by making
measurements in a neighborhood of a timelike geodesic. This problem
arises in an attempt to find the metric of the Universe by observing
light sources or gravitational waves in a neighborhood of a worldline
of an observer. In our analysis we use some of the many tools
developed by Melrose and collaborators.
-
Gigliola Staffilani (MIT)
A curious phenomenon in wave turbulence theory
In this talk we will use the periodic cubic nonlinear Schrödinger equation to present some estimates of the long time dynamics of the energy spectrum, a fundamental object in the study of wave turbulence theory. Going back to Bourgain, one possible way to conduct the analysis is to look at the growth of high Sobolev norms. It turns out that this growth is sensitive to the nature of the space periodicity of the system. I will present a combination of old and very recent results in this direction.
-
Colin Guillarmou (Université Paris-Saclay and CNRS)
On Virasoro conformal blocks with central charge $c>25$ and representation of mapping class group
Conformal blocks are holomorphic sections of bundles over Teichmüller space obtained from the representation theory of Virasoro algebra. In the most simple case, they appear as hypergeometric functions and in general they solve some partial differential equations. They constitute the building blocks for conformal field theories, and a basis for quantization of Teichmüller and moduli spaces, they generate (projective) representations of the mapping class group. Their rigorous construction is involved. We shall explain how a combination of probabilistic and analytic (scattering theory) methods allow us to perform such construction. Based on joint work with Baverez, Kupiainen, Rhodes.
-
Maciej Zworski (UC Berkeley)
Optimal enhanced dissipation for geodesic flows
We consider geodesic flows on negatively curved compact manifolds or more generally contact Anosov flows. The object is to show that if $ X $ is the generator of the flow and $ \Delta$, a (negative) Laplacian, then solutions to the convection diffusion equation, $ \partial_t u = X u + \nu \Delta u $ satisfy $ \| u(t) - \underline u \|_{L^2} \leq C \nu^{-K} e^{-\beta t } \| u(0) \|_{L^2} $ where $ \underline u $ is the (conserved) average of $ u ( 0 ) $ with respect to the contact volume form and $ K $ is a fixed constant. This provides many examples of very precise optimal enhanced dissipation in the sense of recent works of Bedrossian–Blumenthal–Punshon–Smith and Elgindi–Liss–Mattingly. The proof is based on results by Dyatlov and the speaker on stochastic stability of Pollicott–Ruelle resonances. The radial estimates introduced by Melrose in the context of scattering theory on asymptotically Euclidean manifolds are the crucial component of the proof of that result. The talk is based on joint work with Zhongkai Tao.