Schedule

Note: talks in a 90-minute time slot will consist of 30 minutes of lecture, 30 minutes of discussion in breakout rooms, and another 30 minutes of lecture.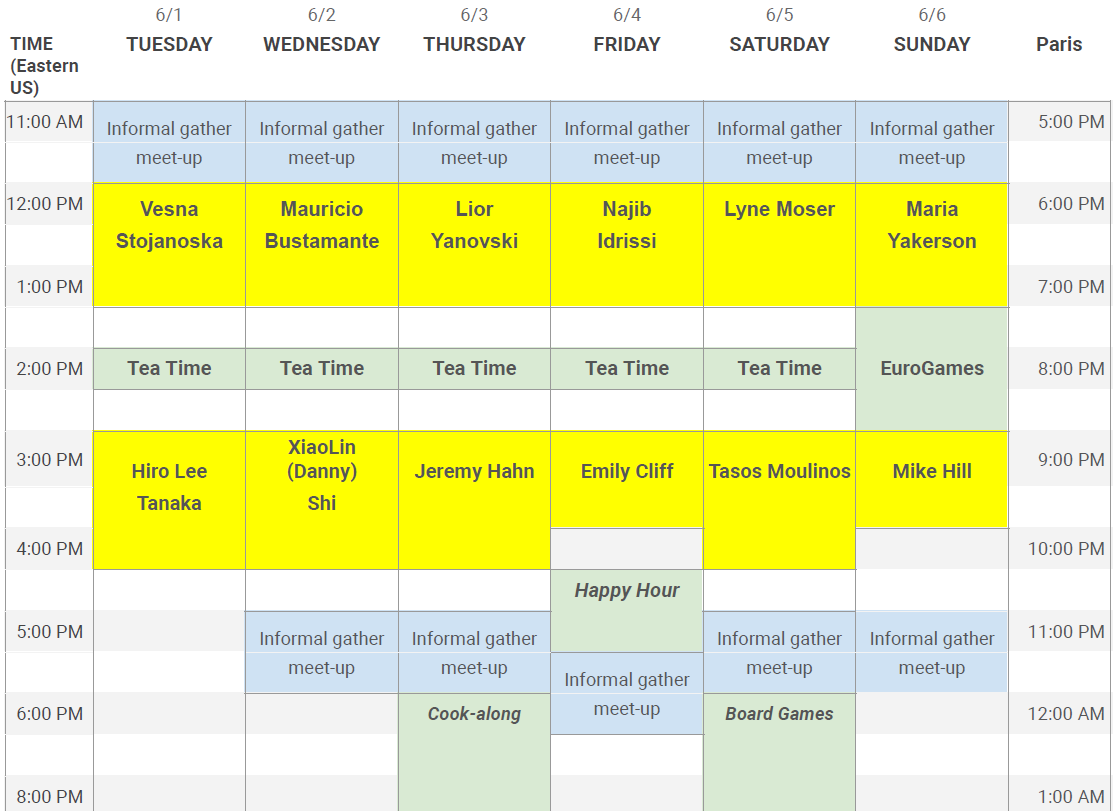

Speaker	Institution	Talk title & abstract	Associated Talbot
Vesna Stojanoska	UIUC	Invertible objects in stable homotopy theory	N/A
		Just like in algebra, a commutative ring spectrum has its associated units, its Picard group, its Brauer group, and they all contain interesting information about the arithmetic of the ring. I will given an overview of these objects, the roles they play in stable homotopy, and hopefully touch on some of the questions and mysterious behaviors surrounding them.
Hiro Tanaka	Texas State University	Viva Fukaya	2009
		It has been twelve years since the 2009 Talbot, where I first learned about Fukaya categories as a first-year graduate student. Twelve years later, it amazingly seems that symplectic geometry has a lot to say about stable homotopy theory, and vice versa, through passageways that are illuminated through Fukaya categories and their variants. Who knows how this talk will go, but I will try to talk about developments since 2009--biasedly focusing on my joint works with Nadler, with Lurie, and with Lazarev-Sylvan--while giving some feel for why people care about Fukaya categories.
Mauricio Bustamante	University of Cambridge	Finiteness properties of moduli spaces of high-dimensional manifolds	2019
		The cohomology and homotopy groups of moduli spaces of smooth manifolds are some of the most basic invariants of manifold bundles: the former contain all the characteristic classes and the latter classify smooth bundles over spheres. Complete calculations of these groups are challenging, even for the simples compact manifolds. It is then desirable to know, at least, some qualitative information, for example whether these groups are (degreewise) finitely generated. In this talk, I will discuss a method to attack this question which leads to the following theorem: if M is a closed smooth manifold of even dimension > 5 with finite fundamental group, then the cohomology and higher homotopy groups of BDiff(M) are finitely generated abelian groups. This is joint work with M. Krannich and A. Kupers.
Danny Shi	University of Chicago	Real bordism, Real orientations, and Lubin--Tate spectra	2016
		In this talk, I will discuss the Real bordism spectrum and the theory of Real orientations. This is an equivariant refinement of the complex cobordism spectrum and the theory of complex orientations. The Real bordism spectrum and its norms are crucial in Hill--Hopkins--Ravenel's solution of the Kervaire invariant one problem in 2009. I will talk about their solution and explain how the Real bordism spectrum is further creating many connections between equivariant stable homotopy theory and chromatic homotopy theory. These newly established connections allow one to use equivariant machinery to attack classical computations that were long considered unapproachable. This talk contains joint work with Agnès Beaudry, Jeremy Hahn, Mike Hill, Guchuan Li, Lennart Meier, Guozhen Wang, Zhouli Xu, and Mingcong Zeng.
Lior Yanovski	MPIM Bonn	Galois extensions in chromatic homotopy theory	2013
		Chromatic homotopy theory is an approach to "higher algebra" (i.e. ring spectra and variations thereof), which generalizes the classical idea of studying an algebraic object by localizing it with respect to various primes. In classical algebra, one can further simplify a local object by considering Galois extensions of the base field (or commutative ring). In his celebrated monograph, Rognes generalized the notion of "Galois extensions" to "higher algebra" and provided the fundamental examples and properties of such extensions. Furthermore, the Galois theory of the chromatic localizations has been completely worked out thanks to the work of Devinats-Hopkins, Rognes, Mathew, and Baker-Richter. After reviewing this story, I will also outline some recent developments by Schlank, Carmeli and myself, in the Galois theory of the, closely related but more difficult to approach, telescopic localizations using the theory of higher semiadditive (a.k.a. ambidexterity) of Hopkins-Lurie.
Jeremy Hahn	MIT	Methods and mysteries in the construction of ring spectra	2017
		Key to the solution of the Kervaire invariant 1 problem was the construction of a certain 'designer' EO cohomology theory. I will survey the techniques, based on work of innumerable homotopy theorists, used to construct BP, tmf, K(n), EO and other designer, structured ring spectra. I will end with recent work building an E3 form of BP<n>, joint with Dylan Wilson, and many open questions.
Najib Idrissi	Université de Paris	Little disks operads and configuration spaces	2015
		Operads are objects that govern categories of algebras. Initially introduced in the sixties to study iterated loop spaces, they have proved useful in several areas of mathematics. In most of these applications, the little disks operads play a central role. In the first part of this talk, we will focus on one of the applications studied in the 2015 Talbot Workshop, Goodwillie--Weiss embedding calculus, which will serve as an ``excuse'' to introduce operads. In the second part of this talk, I will set out some of the recent developments regarding the links between the little disks operads and the real homotopy types of configuration spaces of manifolds. (Second part based on joint works with Ricardo Campos, Julien Ducoulombier, Pascal Lambrechts, and Thomas Willwacher.)
Emily Cliff	University of Sydney/UIUC	The mathematics of 2D conformal field theory	2008
		There are three approaches to the mathematics of conformal field theory: vertex algebras, chiral (or factorization) algebras, and factorizable cosheaves. These notions are also of interest as mathematical objects in their own right, and have provided insight into longstanding problems in representation theory and group theory. Each approach uses ideas and techniques from different areas of mathematics (for example, algebra, analysis, and algebraic or differentiable geometry), and hence has different strengths and weaknesses. In this talk, we will introduce, explore, and compare the three perspectives and the relationships between them. No previous knowledge of the subject is assumed.
Lyne Moser	MPIM Bonn	Defining limits in the ∞-world	2018
		An (∞,1)-category has been shown to support most theorems and constructions of category theory and, by results of Riehl and Verity these categorical constructions do not depend on the model of (∞,1)-categories considered. In the first part of my talk, I will focus on the construction of limits in different models of (∞,1)-categories, which were defined either as terminal objects in the (∞,1)-category of cones or as limits enriched over ∞-groupoids. I will then explain how these notions of limits compare when passing from one model to another. Going one dimension up, a good notion of limits in a 2-category is that of 2-limits, defined as limits enriched over categories. Unlike their 1-categorical analogue, 2-limits do not admit a characterization in terms of 2-terminal objects in a 2-category of cones. Instead, we need to construct a ``shifted'' 2-category of cones to formulate such a theorem. This issue extends to the ∞-setting, and therefore defining limits in an (∞,2)-category is more involved than in the (∞,1)-categorical case. In the second part of the talk, I will explain how to construct limits in the model of (∞,2)-categories given by Rezk's Theta-2-spaces and formlate conjectures on how this construction should compare to the notion of limits enriched over (∞,1)-categories. The results in the 2-categorical setting are joint work with tslil clingman, while those in the ∞-setting are work in progress with Nima Rasekh and Martina Rovelli.
Tasos Moulinos	CNRS	Perspectives on nonabelian Hodge theory	2011
		The nonabelian Hodge correspondence provides a rich interplay of structures from topology, analysis and algebraic geometry which has spurred the curiosities of specialists and non-specialists alike. In the first part of this talk I will outline the celebrated nonabelian Hodge correspondence, due to Carlos Simpson, identifying certain representations of the fundamental group of a smooth projective complex variety with semistable ``Higgs" bundles. I will discuss the consequences of this identification at the level of moduli spaces parametrizing these objects. Time permitting, I will survey more recent extensions to the characteristic p or p-adic settings. I will begin the second half of the lecture with a discussion of the Hodge filtration on nonabelian cohomology. Understanding the framework of filtrations set forth allows for us to view the nonabelian Hodge correspondence in a general light. Indeed, it becomes a manifestation of the following general question: when is a graded object canonically the associated graded of a filtered object? I will conclude this talk with a discussion of some work of mine bringing this perspective into the setting of higher algebra and higher categories, along with joint work with Robalo and Toën applying this perspective towards an understanding of the HKR filtration on Hochschild homology.
Maria Yakerson	ETH Zürich	Avatars for algebraic K-theory in the motivic gather.town	2014
		In this talk, we will design the motivic gather.town, invite algebraic K-theory to join the game and discuss different geometric avatars that we can offer. Warning: the game uses a lot of imagination, so bring your charger with you!
Mike Hill	UCLA	What is Talbot if not friendships persevering?	N/A
		Talbot has been an important part of my academic life, and it has deeply influenced not only my mathematics but also the way I engage with out community. For me, mathematics is a community endeavor, and Talbot provided space for me to grow as a mathematicians. This talk will be a little different than many math talks. I will discuss a theorem: the action of the finite subgroups of the Morava stabilizer group on the Lubin—Tate deformation ring has a particularly nice description. But I will also discuss the false starts, the frustrations, the side roads, and the consequences. For me, this theorem in inextricably intertwined with Talbot, and I will frame and ground the problem in that Talbot story. And along the way, I’ll share a few bits of Talbot history.