Monday, January 7: Prof Vadim Gorin
Persistent random walk and the telegraph equation
Abstract: We will discuss how the evolution of a random walker on the square grid leads to a second order partial differential equation known as the telegraph equation.
Exercises:
Wednesday, January 9: Prof Peter Shor
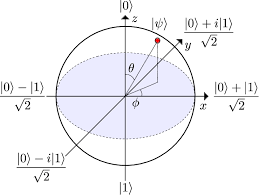
Quantum Weirdness
Abstract: We introduce the basics of quantum mechanics, show how it produces phenomena and probability distributions which cannot be simulated classically, and give some examples of interesting quantum protocols, including the Elitzur–Vaidman bomb tester.
Exercises:
Friday, January 11: Prof Kasso A Okoudjou
Calculus on fractals
Abstract: In this lecture, we will develop some calculus notions on a fractal set. More specifically, we will consider the Sierpinski gasket, and built on it analogs of the trigonometric and polynomial functions. What is remarkable, is that the tools we develop will come from the fractal structure of the Sierpinski gasket.
Exercises:
Monday, January 14: Prof Gilbert Strang
The Functions of Deep Learning
Abstract: We show how the layered neural net architecture of deep learning produces continuous piecewise linear functions as approximations to the unknown map from input to output. A combinatorial formula counts the number of linear pieces in a typical learning function.
Exercises: http://math.mit.edu/~gs/learningfromdata/dsla7-1.pdf, Problems 5, 8 and 18-20 on pages 385-386
Wednesday, January 16: Prof Steven Johnson
Delta functions and distributions
Exercises:
Friday, January 18: Prof John Bush
Surface tension
Abstract: Surface tension is a property of fluid interfaces that leads to myriad subtle and striking effects in nature and technology. We describe a number of surface-tension-dominated systems and how to rationalize their behavior via mathematical modeling. Particular attention is given to the influence of surface tension on biological systems.
Exercises:
Wednesday, January 23: Dr. Jeremy Kepner
Mathematics of Big Data & Machine Learning
Abstract: Big Data describes a new era in the digital age where the volume, velocity, and variety of data created across a wide range of fields (e.g., internet search, healthcare, finance, social media, defense, ...) is increasing at a rate well beyond our ability to analyze the data. Machine Learning has emerged as a powerful tool for transforming this data into usable information. Many technologies (e.g., spreadsheets, databases, graphs, linear algebra, deep neural networks, ...) have been developed to address these challenges. The common theme amongst these technologies is the need to store and operate on data as whole collections instead of as individual data elements. This talk describes the common mathematical foundation of these data collections (associative arrays) that apply across a wide range of applications and technologies. Associative arrays unify and simplify Big Data and Machine Learning. Understanding these mathematical foundations allows the student to see past the differences that lie on the surface of Big Data and Machine Learning applications and technologies and leverage their core mathematical similarities to solve the hardest Big Data and Machine Learning challenges. Supplementary lectures, text, and software are available at: https://mitpress.mit.edu/books/mathematics-big-data
Exercises:
Exercise 1: Derive the gradient descent update algorithm for deep neural networks.
Exercise 2: Write this equation (include the sum over errors) in terms of matrix notation.
Friday, January 25: Prof Justin Solomon
Transport, Geometry, and Computation
Abstract: Optimal transport is a mathematical tool that links probability to geometry. In this talk, we will show how transport can be brought from theory to practice, with applications in machine learning and computer graphics.
Monday, January 28: Prof Scott Sheffield
Tug of War and Other Games
Abstract: I will discuss several games whose analysis involves interesting mathematics. First, in the mathematical version of tug of war, play begins at a game position $x_0$. At each turn a coin is tossed, and the winner gets to move the game position to any point within $\epsilon$ units of the current point. (One can imagine the two players are holding a rope, and the ``winner'' of the coin toss is the one who gets a foothold and then has the chance to pull one step in any desired direction.) Play ends when the game position reaches a boundary set, and player two pays player one the value of a "payoff function" defined on the boundary set.
So... what is the optimal strategy? How much does player one expect to win (in the $\epsilon \to 0$ limit) when both players play optimally? We will answer this question and also explain how this game is related to the "infinity Laplacian," to "optimal Lipschitz extension theory" and to a random turn version of a game called Hex.
Wednesday, January 30: Dr. Chris Rackauckas
The Mathematics of Biological and Pharmacological Systems
Abstract: Biology and pharmacology are many times thought of as non-mathematical disciplines. In modern research practice that is hardly the case. In this talk we will discuss the applications of mathematics to the areas of systems biology and pharmacokinetic/pharmacodynamic modeling. Examples such as spatial pattern formulation (zebra stripes) via Turing instability of partial differential equations, controlling intrinsic biological randomness through stochastic differential equations, and individualized drug dosing and choice optimizations through nonlinear mixed effects models will be introduced. The student will leave with a new lens on how the mathematics they explored in the IAP can be applied to new disciplines which themselves uncover new mathematical problems.
Exercises:
Exercise 1: The Lotka-Volterra system is a predator-prey system which models the interaction of a predator (wolves) and its prey (rabbits). It is given by the ordinary differential equations
x' = ax - bxy
y' = -cy + dxy
where [a,b,c,d] = [1.5,1.0,3.0,1.0]. Solve this equation with [x0,y0] = [1.0,1.0] using a numerical differential equation solver (I recommend using Julia, see http://docs.juliadiffeq.org/latest/tutorials/ode_example.html as a tutorial). Describe the output behavior of this system.
Exercise 2: Many of the difficult test cases in numerical differential equations come from the field of mathematical biology. The ROBER equations is one such example, described by the system:
y1' = -k1*y1 + k3*y2*y3
y2' = k1*y1 - k2*y2^2 - k3*y2*y3
y3' = k2*y2^2
where [k1,k2,k3] = [0.04,3x10^7,10^4]. Use a numerical solving software to test out two different methods, an explicit Runge-Kutta method and a method for stiff equations (e.g. in Julia, Tsit5() vs Rosenbrock23(), or MATLAB ode45 vs ode15s) and see how the solution timing differs, or if one of the methods fails to solve the equation. This concept of stiffness tends to occur when models have mechanisms acting on different time scales. What about this model is causing the issue?