The Imaging and Computing Group (ICG) studies inverse problems related to wave scattering and high-frequency data.
The group‘s research directions are in the areas of machine learning, scientific computing, applied harmonic analysis, and recovery theory. The problems we consider are often motivated by real-life questions in seismic imaging.
We are always on the lookout for talented people to join the group!
Research Highlights
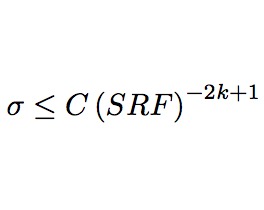
When is superresolution of sparse signals possible? We quantify regimes of stable super-resolved recovery of sparse signals from bandlimited measurements. In the case of adversarial deterministic ...read more
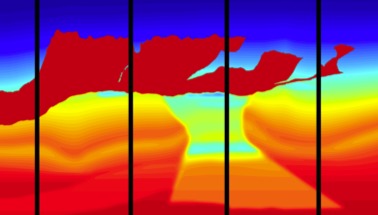
A scalable solver for the Helmholtz equation. We present a numerical method for the 2D high-frequency Helmholtz equation with online parallel complexity that scales sublinearly as O(N/L), where N is ...read more
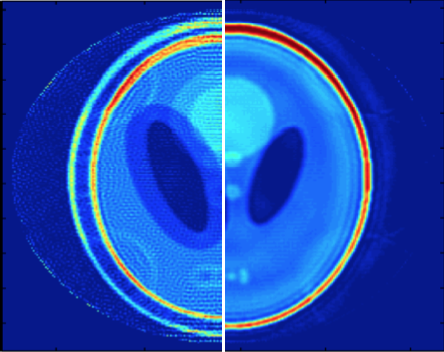
Convex recovery from interferometric measurements. We show a deterministic stability result for the recovery of vectors from interferometric measurements, which have important applications in ...read more

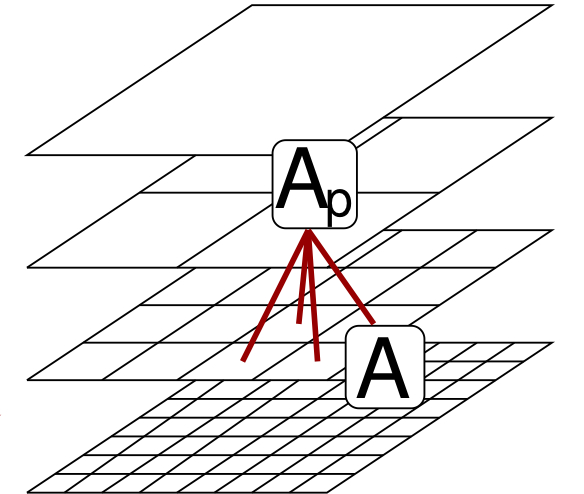
Matrix probing: randomized fitting for the wave-equation Hessian. What can be determined about the pseudoinverse pinv(A) of a matrix A from one application of A to a vector of random entries? A ...read more
A butterfly algorithm for synthetic aperture radar imaging. We propose what is perhaps the first O(N log N) controlled-accuracy algorithm for SAR imaging. We use the butterfly scheme, an alternative to ...read more

Wave computation with Fourier integral operators. We propose a new time upscaling method to avoid the CFL condition for acoustic wave propagation in a smooth heterogeneous medium, by numerically ...read more