Professor Laurent Demanet

Imaging and Computing Group

The Imaging and Computing Group (ICG) works across many areas of computational mathematics and physics, including inverse problems in the context of wave scattering and high-frequency data.

The group‘s research directions include scientific AI, computational methods for PDE, applied harmonic analysis and signal processing, and statistical inverse problems. The problems we consider are often motivated by real-life questions in geophysics, such as seismic imaging.

We are always on the lookout for talented people to join the group!

Research Highlights

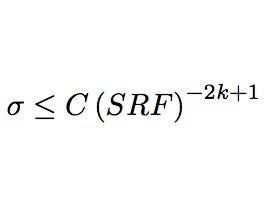
When is superresolution of sparse signals possible?

We quantify regimes of stable super-resolved recovery of sparse signals from bandlimited measurements. In the case of adversarial deterministic noise of magnitude sigma, for a system of low-frequency sinusoids with large super-resolution factor SRF (inverse bandwidth over grid spacing), we show that recovery of any k-sparse signal holds in the regime shown in the picture, without additional spike spacing assumption. This rate is tight in the minimax sense: no method can recover all k-sparse signals with higher noise levels. Compressed sensing (ell_1 minimization) generally operates at the Shannon-Nyquist rate (SRF less than 1), hence is suboptimal for this task. Paper with Nam Nguyen.

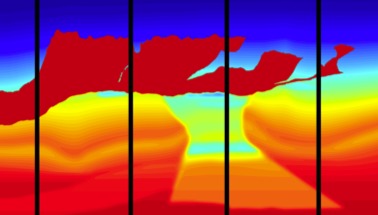
A scalable solver for the Helmholtz equation.

We present a numerical method for the 2D high-frequency Helmholtz equation with online parallel complexity that scales sublinearly as O(N/L), where N is the number of volume unknowns, and L is the number of processors, as long as L is a small fractional power of N. The solver decomposes the domain into L layers, and uses transmission conditions in boundary integral form to explicitly define "polarized traces", i.e., directional waves sampled at interfaces. Local direct solvers are used in each layer to precompute traces of local Green's functions in an embarrassingly parallel way (the offline part), and incomplete Green's formulas are used to propagate interface data in a sweeping fashion, as a preconditioner inside a GMRES loop (the online part). The favorable scalability owes to the availability of fast algorithms for the integral kernels. Paper with Leonardo Zepeda-Nunez.

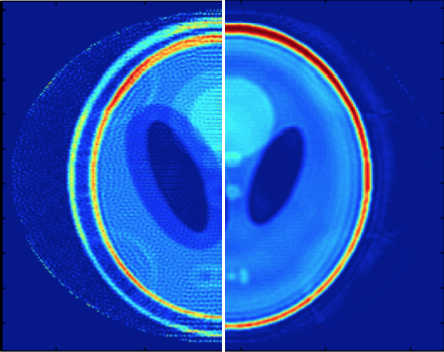
Convex recovery from interferometric measurements.

We show a deterministic stability result for the recovery of vectors from interferometric measurements, which have important applications in model-robust imaging from scattered waves. The connectivity of the underlying graph determines the stability constant via the spectral gap of the graph Laplacian. 'Paper 1 and Paper 2, with Vincent Jugnon.

Matrix probing: randomized fitting for the wave-equation Hessian.

What can be determined about the pseudoinverse pinv(A) of a matrix A from one application of A to a vector of random entries? A surprising lot, provided pinv(A) is known to belong to a "good" vector subspace. This approach offers a compelling preconditioner for the wave-equation Hessian (normal operator) in seismic imaging. The performance guarantees follow from large deviation estimates of independent interest. Paper with P. Letourneau, N. Boumal, H. Calandra, J. Chiu, and S. Snelson.

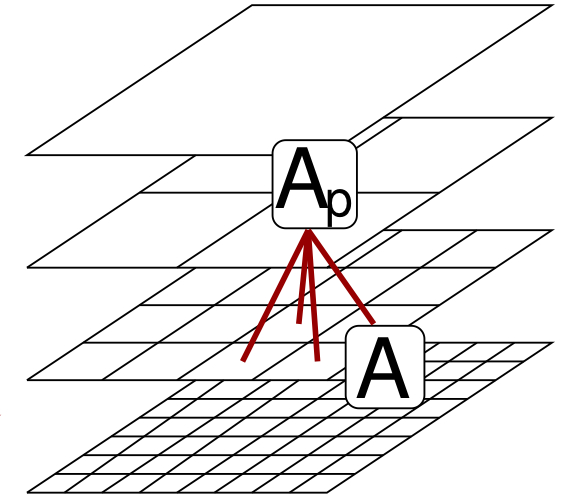
A butterfly algorithm for synthetic aperture radar imaging.

We propose what is perhaps the first O(N log N) controlled-accuracy algorithm for SAR imaging. We use the butterfly scheme, an alternative to the FFT which works for much more general oscillatory integrals than the Fourier transform. With M. Ferrara, N. Maxwell, J. Poulson, and L. Ying. The paper is here, and a version of the software is available here.

Wave computation with Fourier integral operators.

We propose a new time upscaling method to avoid the CFL condition for acoustic wave propagation in a smooth heterogeneous medium, by numerically representing the Green's function as a sum of Fourier integral operators. The method hinges on handling pseudodifferential symbols via discrete symbol calculus, and Fourier integrals using any of the fast methods that have recently been developed for their fast computation. With L. Ying. The paper is here.