A unified introduction to the theory and practice of modern, near linear-time, numerical methods for large-scale partial-differential and integral equations. Topics include: preconditioned iterative methods; generalized Fast Fourier Transform and other butterfly-based methods; multiresolution approaches including multigrid algorithms, hierarchical low-rank matrix decompositions, and low and high frequency Fast Multipole Methods. Example applications include: aircraft design, cardiovascular system modeling, electronic structure computation, and tomographic imaging.
Grad H subject. Units: 3-0-9. The class is suitable for graduate students from all departments who have affinities with mathematics.
Topics:
Introduction: PDE vs. integral equations, Fourier-based numerical
methods.
Exterior problems:
- Surface integral equations, layer potentials
- The Fast Multipole Method (FMM)
- Partitioned low-rank methods, skeletons, cross-approximation
- Applications to electrostatics, biomolecules, potential flows
Interior problems and variable media:
- Multigrid and relaxation
- Volume integral equations
- Applications to fluid and heat flows, dieletrics, electronic density
High-frequency problems:
- High-frequency FMM
- Butterfly algorithms
- Applications to acoustic and electromagnetic scattering, radar imaging
Prerequisites: Some familiarity with ordinary differential equations, partial differential equations, Fourier transforms, linear algebra, and basic numerical methods for PDE, at the level of 18.085. The assignments will involve computer programming in the language of your choice (Matlab recommended).
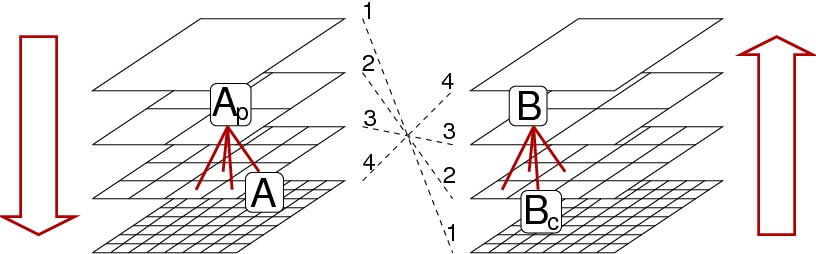
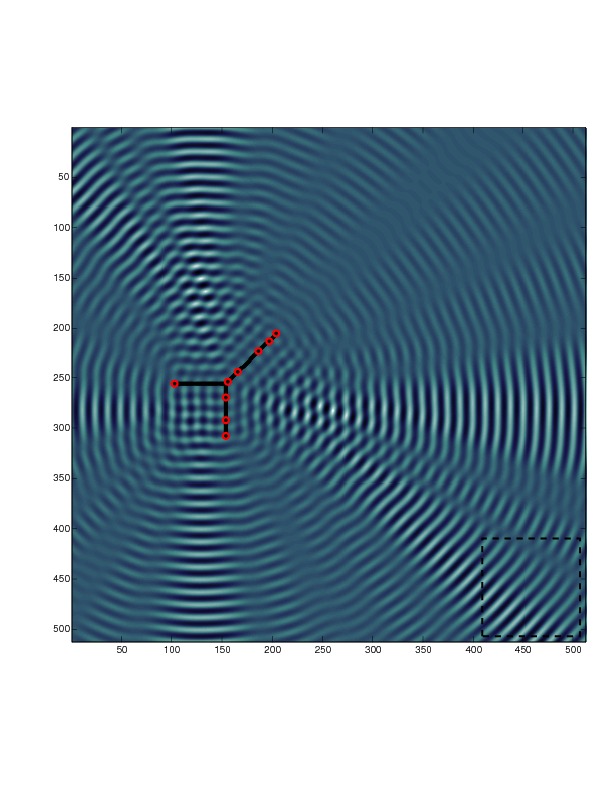
Figures: top-right, the hierarchical tree structure of the butterfly algorithm. Bottom-left, low-rank interactions in the electromagnetic far-field
Here is the current version of the class notes: 04/23/2014
Some material from last year:
- Notes from Richard Zhang for the first few lectures: set 1, set 2, set 3.
- A first set of handwritten notes on the fast multipole method, boundary integral equations, h-matrices, and the butterfly algorithm.
- A second set of handwritten notes on multigrid.
Good references on the fast multipole method: review article by Ying, review article by Beatson and Greengard, Ying et al. paper on the kernel-independent FMM.
Some basic Matlab scripts for solving PDE:
- Poisson equation: run_poisson.m, solve_poisson_jacobi.m.
- Sparse matrix for the 2D Dirichlet Laplacian: poisson2d_dirichlet.m.
- Heat and advection equations: heat_EE.m, heat_CN.m, adv_EE.m, adv_LF.m.
Three references books covering background material on numerical methods for PDE.
- R. LeVeque, Finite difference methods for ordinary and partial differential equations, SIAM, 2007.
- N. Trefethen, Spectral methods in Matlab, SIAM, 2000.
- R. LeVeque, Finite volume methods for hyperbolic problems, Cambridge University Press, 2002.
Date and Time: Tu-Th, 1:00-2:30, room 4-159.
Instructors: Laurent Demanet and Jacob White.
TA: Carlos Sauer-Ayala, csauer@math.mit.edu.
Office hours: Laurent Demanet: W-F, 2:00-4:00, room E17-414. Else, email the instructors.
50% homework, 50% course project.
The homework problem sets will consist of both theoretical problems and numerical experiments. No late copy will be allowed. The lowest score will be dropped. Collaboration is allowed, but the codes and copies you turn in must be original and written by you.
- Problem set 1: due 02/27. Sparse solver for the 2D Dirichlet Laplacian: here. MRI permittivity model: right-click and download the 257 x 257 dataset, and the 1025 x 1025 dataset. DST code in 1D: dst1.m.
- Problem set 2: due 03/20.
- Problem set 3: due 04/17. Here is nwspgr.m and the latest version of DEMCEM (for reference, here is last year's DEMCEM).
- Problem set 4: due 05/08. Here is solvepoissonmultigrid.m.
The course project will be of a computational or mathematical nature. Each student will have a different project (hopefully tailored to their taste). The project report should be written like a publication: clear and concise. It is a good idea to use LaTeX for the typesetting. Here is a list of possible project topics.
Important dates:
- Choose a project by early March. Requires consent of the instructor.
- Progress checkup: early April (schedule a meeting with the instructor).
- Project presentations: 05/13 and 05/15.
- Project report due: 05/15.