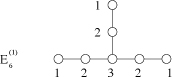
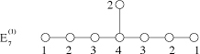
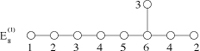
Click here for the Conference schedule.

Tomoyuki Arakawa (Nara Women's University, Japan)
"Representations of W-algebras and conjectures of Kac-Wakimoto"
Abstract:
In my talk I will discuss the representation of affine W-algebras, in particular, the conjectures of Kac-Wakimoto on the "minimal series" representation of W-algebras.

Bojko Bakalov (North Carolina State University)
"Vertex algebras in higher dimensions and local actions of Lie algebras on vertex algebras"
Abstract:
The notion of a vertex algebra in dimension D differs from the usual one by replacing the formal variable z with a vector z=(z^1,~E,z^D) and expressions like z-w with the square length of the vector z-w. When equipped with an action of the Lie algebra c_D of infinitesimal conformal transformations, such vertex algebras arise in globally conformal invariant quantum field theory in dimension D. From a vertex algebra in dimension D one can obtain a usual (D=1) one via the restriction z=(x,0,~E,0). The action of the Lie algebra c_D then gives a local action on this vertex algebra.
In this talk, I will start with a general discussion of local actions of Lie algebras on vertex algebras. Even though it is ubiquitous, this notion seems new. Then I will state a theorem, obtained jointly with N.M. Nikolov, that any vertex algebra equipped with a local, integrable, positive-energy action of c_D can be obtained as the restriction of some conformal vertex algebra in dimension D.

Vyjayanthi Chari (University of California, Riverside)
"Abelian ideals, current algebras and Koszul algebras"
Abstract:
For suitable subsets S of set of positive roots (for example, maximal abelian ideals in types A or C) of a complex simple Lie algebra, and finite subsets F of the dominant integral weights, we define a finite--dimensional graded associative algebra A(F, S). We show that the module category of this algebra is naturally equivalent to a category of representations of the corresponding truncated current algebra of the simple Lie algebra. As a consequence, we prove that A(F, S) is a Koszul algebra. We then show that we can define the direct limit A(S) of these algebras and prove that A(S) is an infinite dimensional Koszul algebra. An example of an algebra which arises from our construction is a one point extension of the Auslander-Reiten quiver of type A^\infty_\infty. This is based on joint work with Jacob Greenstein.

William Crawley-Boevey (University of Leeds, UK)
"The Deligne-Simpson problem"
Abstract:
Given some conjugacy classes in the general linear group, theDeligne-Simpson problem asks whether or not there are matrices in theseclasses whose product is the identity, and with no common invariantsubspace. I shall survey some of my work on this and related problems,explaining the role of Kac's Theorem on representations of quivers,Kac-Moody Lie algebras, and loop algebras of Kac-Moody Lie algebras.

Thibault Damour (IHES, France)
"Chaos and Symmetry in Gravity and Supergravity"
Abstract:
We shall review the intriguing connection between the Belinsky-Khalatnikov-Lifshitz-type 'chaotic' behaviour of spacelike singularities in gravity and supergravity, and certain hyperbolic Kac-Moody algebras (notably E_10). This leads to studying a one-dimensional E_10 coset model. This study hints at an 'hyperbolic' generalization of the usual (affine Kac-Moody) Sugawara construction.

Corrado De Concini (University of Rome "La Sapienza", Italy)
"Partition functions and transversally elliptic differential operators"
Abstract:
Joint with C. Procesi and M. Vergne. This talk is about certain spaces originally introduced by W. Dahmen and C. Micchelli motivated by facts in Numerical Analisys and some generalizations. This spaces are useful to prove the quasi polinomiality of partition functions.
Let G be a compact abelian Lie group, M a complex G module, M_{> i} the open set of vectors whose orbit has dimension at least i. These spaces appear as the K_G-theory of the spaces T_G M_{> i} of cotangent vectors vanishing on vector tangent to orbits. This completes an old project of Atiyah and Singer related to the computation of the index of tranversally elliptic operators.

Giovanni Felder (ETH, Switzerland)
"Riemann-Roch-Hirzebruch formulae for traces of differential operators"
Abstract:
The Lefschetz number of a holomorphic differential operator acting on sections of a vector bundle on a compact complex manifold is the alternating sum of traces of the induced map on cohomology. The Feigin-Shoikhet conjecture (now a theorem) expresses the Lefschetz number of an operator D as the integral over the manifold of a differential form depending locally on D and on a chosen connection. When D is the identity, the formula reduces to the Riemann-Roch-Hirzebruch formula, with the Chern-Weil representative of the characteristic class. In the case of a compact group action there are localization formulae expressing the Lefschetz number as an integral over fixed point sets. This talk is based on joint papers with B. Feigin and B. Shoikhet, with M. Engeli and with X. Tang.

Edward Frenkel (University of California, Berkeley)
"Opers with irregular singularity and shift of argument subalgebra"
Abstract:
The universal enveloping algebra of any simple Lie algebra g contains a family of commutative subalgebras, called the quantum shift of argument subalgebras. Recently B. Feigin, L. Rybnikov and myself have proved that generically their action on finite-dimensional modules is diagonalizable and their joint spectra are in bijection with differential geometric objects on the projective line called "opers". They have regular singularity at one point, irregular singularity at another point and are monodromy free. Interestingly, they are associated not to G, but to the Langlands dual group of G. In addition, we have shown that the quantum shift of argument subalgebra corresponding to a regular nilpotent element of g has a cyclic vector in any irreducible finite-dimensional g-module. As a byproduct, we obtain the structure of a Gorenstein ring on any such module. I will talk about these results and explain the connection to the geometric Langlands correspondence.

Dennis Gaitsgory (Harvard University)
"The Kazhdan-Lusztig equivalence (quantum groups vs. affine algebras), revisited"
Abstract:

Reimundo Heluani (University of California, Berkeley)
"Supersymmetry of the Chiral de Rham complex"
Abstract:
The "chiral de Rham complex" of Malikov-Shechtman-Vaintrob is a sheaf of vertex superalgebras associated to any manifold X. We will show how, in the smooth context, extra geometric data on X (e.g. having special holonomy) translates into extra symmetries of the corresponding vertex superalgebras of global sections.

David Kazhdan(Hebrew University, Jerusalem, Israel)
"Satake isomorphism for Kac-Moody algebras"
Abstract:
I will define the spherical Hecke algebra for (untwisted) affine Kac-Moody groups, and prove a generalization of the Satake isomorphism for these algebras, relating them to integrable representations of the Langlands dual affine Kac-Moody group.

Bertram Kostant (MIT)
"On some of the mathematics in Garrett Lisi's E(8) Theory of Everything"
Abstract:
A physicist , Garrett Lisi , has published a highly controversal, but fascinating, paper purporting to go beyond the standard model in that it unifies all 4 forces of nature by using as gauge group the exceptional Lie group E(8). My talk, strictly mathematical, will be about an elabloration of the mathematics of E(8) which Lisi relies on to construct his theory.

Roberto Longo (University of Rome "Tor Vergata", Italy)
"SUSY in the Conformal World"
Abstract:
We make an analysis of superconformal field theory by an operator algebraic point of view. This leads to consider nets of von Neumann algebras on covers of the circle and we explain the structure of the Neveu-Schwarz and Ramond representations. A formula involving both Fredholm and Jones index appears. The net associated with the super-Virasoro algebra is constructed and all superconformal nets in the discrete series c <3/2 are classified. We construct a spectral triple with a first computation of the associated Connes cyclic cohomology. (Based on a Joint work with S. Carpi and Y. Kawahigashi)

Olivier Mathieu (University of Lyon "Claude-Bernard", France)
"Varieties determined by their jets"
Abstract:
TBA

Werner Nahm (Dublin Institute for Advanced Studies, Ireland)
"Quantum groups, modular forms, and integrable quantum field theories"
Abstract:
Affine Kac-Moody algebras allowed for the first time a good understanding of quantum field theories beyond the free case, briding a long-standing gap between mathematics and physics. The theories turned out to have very beautiful mathematical structures. Their integrable deformations promise an equally rich harvest, as exemplified by connections between the scattering matrix, the Bethe ansatz and the discrete Hirota equations on one hand and modular forms, Yangians and algebraic K-theory on the other.

Andrei Okounkov (Princeton University)
"Vertex operators in gauge theory"
Abstract:
TBA

Paolo Papi (University of Rome 'La Sapienza',Italy)
"On the kernel of the affine Dirac operator"
Abstract:
Let g be a finite-dimensional semisimple Lie algebra with a non-degenerate invariant bilinear form (.,.), s a diagonalizable automorphism of g leaving the form (.,.) invariant, and h an s-invariant subalgebra of g, such that the restriction of the form (.,.) to h is non-degenerate. Let L^ (g,s) and L^ (h,s) be the associated twisted affine Lie algebras and F^s(p) the s-twisted Clifford module over L^ (h ,s), associated to the orthocomplement p of h in g. Under suitable hypotheses on s and g, we provide a general formula for the decomposition of the kernel of the affine Dirac operator, acting on the tensor product of an integrable highest weight L^ (g,s)-module and F^s(p), into irreducible L^ (a, s)-submodules. I'll discuss applications to decomposition of all level 1 integrable irreducible highest weight modules over orthogonal affine Lie algebras with respect to the affinization of the isotropy subalgebra of an arbitrary symmetric space and to formulas for asymptotic dimension. This is a joint work with Kac and Moseneder Frajria.

Alexander Premet (University of Manchester, UK)
"Finite W-algebras and sheets in semisimple Lie algebras"
Abstract:
The ideals of codimension 1 of a finite W-algebra W=W(g,e) are parametrized by the points of an affine algebraic variaety X. In my talk I will show how to compute the dimension of X in the case where g is classical (and in many other cases). An interplay between the characteristic zero theory and the characteristic p theory will also be discussed.

Alexei Rudakov (NTNU, Norway)
"Morphisms of Verma modules for E(5,10)"
Abstract:
The Lie superalgebra L = E(5, 10) is an infinite dimensional graded superalgebra: L = Sum_{j >=-2} p_j , where p_0= sl_^@5(C) and the p_0 -modules occurring in the negative part are: p_1 = \Wedge^2 C^5, p_2 = (C5)^*. The generalized Verma modules for E(5, 10) and some of their morphisms were first considered in [Kac, Rudakov, 2002]. Since then new morphisms were found and we have come to the better understanding of the situation. In the talk we define the degree of a morphism of (generalized) Verma modules for a graded Lie superalgebra like L above. We show that the morphisms found in [Kac, Rudakov, 2002] are in fact all the morphisms of degree 1 between Verma modules for E(5, 10). Currently more morphisms are known. We show that there exist morphisms with degrees less or equal to 5. We also discuss how the morphisms are combined naturally into complexes and what are known about these complexes.

Vera Serganova (University of California, Berkeley )
"Characters of affine Lie superalgebras and 'super Weyl group'"
Abstract:
The famous Weyl character formula was generalized by V. Kac to an arbitrary symmetrizable Kac-Moody algebra. In the case of Lie superalgebras a uniform character formula does not exist even for finite-dimensional simple superalgebras. In some cases however there is a beautiful formula conjectured by Kac and Wakimoto (it has nice applications in super affine case). I will prove this formula for certain affine superalgebras. As in Kac-Moody case the proof uses only the existence of the Casimir operator and W-invariance of the character. But W is not a group anymore.

Ivan Todorov (Institute of Nuclear Research and Nuclear Energy, Bulgaria)
"CFT METHODS IN FOUR DIMENSIONAL CONFORMAL FIELD THEORY"
Abstract:
It is often argued that 2-dimensional conformal field theory (2D CFT) is too special to expect that its methods will work in four space-time dimensions (4D). We shall demonstrate that most objections can, in fact, be overcome. Using, in particular, the principle of global conformal invariance (GCI) in Minkowski space one can extend the notion of a (chiral) vertex algebra to higher dimensions. Although there are no scalar Lie fields in more than two dimensions, harmonic bilocal fields, which naturally arise in operator product expansions in 4D GCI models, give rise to infinite dimensional Lie algebras so that powerful methods (developed, in particular, by Victor Kac) happily apply. The talk is based on joint work with B. Bakalov, N.M. Nikolov, K.-H. Rehren (and, at an earlier stage, Ya.S. Stanev)

Ernest Vinberg (Moscow State University, Russia)
"On double cosets of a pair of excellent spherical subgroups"
Abstract:
Let G be a simply connected semisimple algebraic group and H∠G be a spherical subgroup. We call H excellent if G/H is quasiaffine and the semigroup of highest weights of the representation G:C[G/H] is generated by disjoint linear combinations of the fundamental weights of G. For example, the following subgroups are excellent: 1) the subgroup of fixed points of any involution of G; 2) any connected semisimple spherical subgroup of a simple group G; 3) a maximal unipotent subgroup U of G. Let F and H be two excellent spherical subgroups of G. Consider the algebra C[F\G/H] of regular functions on G invariant under the left-right action of FxH. Let X=Spec C[G/H], Y=Spec C[F\G], Z=Spec C[F\G/H] and p:X -> Z, q:Y -> Z be the natural morphisms. Then 1) the algebra C[F\G/H] is polynomial; 2) generic fibers of the natural morphism G -> Z are double cosets of the pair (F,H); 3) the morphisms p and q are surjective and equidimensional; 4) each irreducible component of each fiber of p (resp. q) meets G/H (resp. F\G). For F=U the equidimensionality of p was proved by D.Panyushev in 1999 (Canad. J. Math. 51).

Minoru Wakimoto (Kyushu University, Japan)
"Rationality of W-algebras via quantum reduction "
Abstract:
Given a data (g,f,k) where g is a finite-dimensional simple Lie algebra and f is its nilpotent element and k is a complex number called the level, the W-algebra W(g,f)_k is constructed via quantum reduction. In this talk, we will discuss the "minimal series representations" of W(g,f)_k for which, by definition, characters are holomorphic functions and span a finite-dimensional SL(2,Z)-invariant space. This talk is a joint work with Victor Kac.

Efim Zelmanov (University of California, San Diego)
"Jordan Superalgebras"
Abstract:
I will survey the structure and representations of Jordan superalgebras. A special emphasis will be made on the role played by the exceptional superconformal Cheng - Kac superalgebra in this theory.