Schedule 1998 Spring
March 4
Peter Winkler (Bell Labs)
Phase transitions on a tree
Although it is manifestly different from a cubic lattice in Euclidean space, the Cayley tree (or "Bethe Lattice") offers an opportunity to prove theorems about phase transitions, on account of its connection with branching random walks. Modelling hard-constraint systems by random homomorphisms of graphs, we characterize the constraint graphs which exhibit more than one simple invariant Gibbs measure.
Our methods are elementary and no acquaintance with statistical physics will be assumed.
Joint work with Graham Brightwell (London School of Economics).
March 6
Sara Billey (MIT)
Pattern avoidance and rational smoothness of Schubert varieties
Abstract: Let w be an element of the Weyl group S_n, and let X_w be the Schubert variety associated to w in the flag manifold SL_{n}(C)/B. Lakshmibai and Sandhya showed that X_w is smooth if and only if w avoids the patterns 4231 and 3412. Using two tests for rational smoothness due to Carrell, we show that rational smoothness of X_w is characterized by pattern avoidance for types B and C as well. A key step in the proof of this result is a sequence of rules for factoring the Poincare polynomials for the cohomology ring of X_w generalizing the recent work of Gasharov.
March 11
Eva Feichtner (MIT)
On the cohomology algebras of complex subspace arrangements
Abstract: We show that for a complex subspace arrangement with geometric intersection lattice the integral cohomology algebra of the complement is completely determined by the combinatorial data of the arrangement. Our approach relies on a combinatorial encoding of the arrangement's topology into order complexes of posets. We explicitly describe generating cohomology classes on simplicial models for the complement of the arrangement and derive a presentation of its cohomology algebra in the spirit of the combinatorial description of cohomology algebras of complex hyperplane arrangements by Orlik and Solomon.
This is joint work with Gunter M. Ziegler.
March 13
Takayuki Hibi (Osaka University)
Nonregular unimodular triangulations of convex polytopes
It was unknown, for a long time, if there exists a lattice polytope which possesses a unimodular triangulation and none of whose unimodular triangulations is regular. The purpose of my talk is to present a family ${\cal F}$ of $(0,1)$-polytopes such that each polytope belonging to ${\cal F}$ has a unimodular triangulation, but has no regular unimodular triangulation. This is a joint work with Hidefumi Ohsugi.
March 18
Alex Suciu (Northeastern University)
Characteristic varieties of real and complex arrangements
The k-th Fitting ideal of the Alexander invariant of an arrangement A of n complex hyperplanes defines a characteristic subvariety, V_k(A), of the complex algebraic torus (C^*)^n. The characteristic varieties of an arrangement provide subtle and effectively computable homotopy-type invariants of its complement. In joint work with Daniel Cohen, we show that the tangent cone at the identity of the top characteristic variety V_1(A) coincides with R_1(A), the first-cohomology support locus of the Orlik-Solomon algebra. We conclude that the variety V_1(A) is combinatorially determined, and that Falk's variety R_1(A) is the union of a subspace arrangement in C^n. We illustrate these techniques by computing the top characteristic varieties of braid arrangements and monomial arrangements.
If A is a real 2-arrangement (in the sense of Goresky and McPherson), the characteristic varieties are no longer subtori through the origin. The nature of these varieties vividly illustrates the difference between real and complex arrangements. In joint work with Daniel Matei, we study the homotopy types of complements of arrangements of n transverse planes in R^4, obtaining a complete classification for n<=6, and lower bounds for the number of homotopy types in general. Furthermore, we show that the homotopy type of the complement of a 2-arrangement in R^4 is not determined by its cohomology ring, thereby answering a question of Ziegler.
The papers on which the talk will be based can be found at http://www.math.neu.edu/~suciu/publications.html.
April 1
Jim Haglund (MIT)
Further investigations involving polynomials with only real roots
Abstract: We present a number of conjectures involving rook polynomials having only real zeros. Many of these generalize a previous conjecture of the author, K. Ono, and D. G. Wagner, namely that if $A$ is a real $n \times n$ matrix which is weakly increasing down columns, then the permanent of $zA+J_n$ has only real zeros. In some cases these conjectures are motivated by factorization theorems for Ferrers boards. Connections between results of Laguerre and Szeg\"o on transformations which send polynomials with only real roots to other such polynomials are discussed. We also present a weighted version of the Poset Conjecture of enumerative combinatorics.
April 3
Manjul Bhargava (Princeton University)
The factorial function... and generalizations
Abstract: Though ubiquitous in combinatorics, the factorial function also occurs surprisingly often in number theory. A close examination of these occurrences leads to a series of beautiful generalizations of the factorial function, which also turn out to be quite useful in a variety of combinatorial, number-theoretic, and ring-theoretic problems. In particular, a fundamental problem about integer-valued polynomials, put forth by P\'olya in 1919, is now resolved.
April 8
Irena Peeva (M.I.T.)
Monomial ideals, real Boolean subspace arrangements, and order dimension of lattices
Abstract: The talk is on a joint work with V. Gasharov, V. Reiner, and V. Welker. We give a formula for the graded Betti numbers of a monomial ideal in terms of the homology of the lower intervals in the lattice of least common multiples of the minimal monomial ideal generators; the formula has the same flavour as the Goresky-MacPherson formula for the dimensions of the cohomology of the complement of a subspace arrangement. This leads to a relation of the cohomological properties of real Boolean arrangements and square-free monomial ideals. Another application of the formula is a relation between the homology and the order dimension of an arbitrary finite lattice.
April 10
Karen L. Collins (Wesleyan University)
Breaking symmetries of S5 and S6
Abstract: A labeling of the vertices of a graph G is said to be r-distinguishing, provided no automorphism of the graph preserves all of the vertex labels. The distinguishing number of a graph G, D(G), is the minimum r such that G has an r-distinguishing labeling. For any group J, we define D(J) := { D(G) | Aut(G) is isomorphic to J }. It has been shown that D(S3) = {2,3}, and D(S4) = {2,4}. In this talk, we will sketch the proof that D(S5) = {2,3,5} and present other distinguishing results.
April 15
Patricia Hersh (M.I.T.)
Shuffle posets of multisets
Abstract: We study posets defined by Stanley as a multiset generalization of Greene's shuffle posets. We compute the flag f-vector in terms of the quasi-symmetric function encoding $F_P$ defined by Ehrenborg. The result is a symmetric function which is expressible as a sum of Schur functions with nonnegative integer coefficients. We find a topological chain decomposition which yields $F_P$ and similarly gives the characteristic polynomial, zeta polynomial and rank generating function for shuffle posets of multisets. This decomposition also leads to a symmetric group action on maximal chains with Frobenius characteristic related to $F_P$.
April 17
Anders Buch (University of Chicago)
Chern class formulas for degeneracy loci
Abstract: We study a general class of degeneracy loci associated to a sequence of vector bundles with maps between them and arbitrary rank conditions on the maps and their compositions. The cohomology classes of such loci are described by polynomials in the Chern classes of the vector bundles. These polynomials generalize all known types of Schubert polynomials. We give explicit formulas for the polynomials as linear combinations with integer coefficients of products of Schur determinants. We furthermore conjecture that all coefficients are positive and given by counting tableaux.
A preprint by Anders Buch and William Fulton is available.
April 22
Andrzej Ruci\'nski (Adam Mickiewicz University, Pozna\'n, Poland and Emory University)
On graphs with linear Ramsey numbers
Abstract: For a fixed graph $H$, the \emph{Ramsey number} $r(H)$ is defined to be the least integer $N$ such that in any 2-coloring of the edges of the complete graph $K_{N}$, some monochromatic copy of $H$ is always formed. Let ${\mathcal H}(n,\Delta)$ denote the class of graphs $H$ having $n$ vertices and maximum degree $\Delta$. It was shown by Chvat\'al, R\"odl, Szemer\'edi and Trotter that for each $\Delta$ there exists $c(\Delta)$ such that $r(H) < c(\Delta)n$ for all $H \in {\mathcal H}(n,\Delta)$. That is, the Ramsey numbers grow \emph{linearly} with the size of $H$. However, their proof relied on the well-known regularity lemma of Szemeredi and only gave an upper bound for $c(\Delta)$ which grew like an exponential tower of $2's$ of height $\Delta$.
In this talk we avoid the use of the regularity lemma altogether, and show that one can in fact take, for some fixed $c$, $c(\Delta) < 2^{c\Delta(\log \Delta)^{2}}$ in the general case, and even $c(\Delta) < 2^{c\Delta\log \Delta}$ if $H$ is bipartite. In particular, we improve an old upper bound on the Ramsey number of the $n$-cube due to Beck \cite{B}. We also show that for all $n$, there are $H' \in {\mathcal H}(n,\Delta)$ with $r(H') > 2^{c'\Delta}n$ for a fixed $c' > 0$, which is not so far from our upper bound.
This is a joint work with R.L.Graham and V.R\"odl.
April 24
Lou Shapiro (Howard University)
Path pairs and Catalan probabilities
Abstract. Path pairs are pairs of paths starting at the origin, each consisting of unit east and north steps, with the upper path never going below the lower path, and with the two rapths having a common endpoint. They are in many ways the mother of all Catalan settings. Togrther with generating functions and k-motzkin paths we can derive probabalistic statements about many Catalan phenomena. For instance as n gets large the number of elements in the visible blocks of a noncrossing partition approaches 8. A variety of such results will be discussed including walking through an Eulerian polygonal maze.
April 29
Henrik Eriksson (KTH, Stockholm)
Sorting bridge hands and DNA
Abstract: Most bridge players start by sorting their hand, repeatedly moving blocks of cards. Open problem: Can this be done in at most seven moves? Solved problem: Sort the reversed permutation in seven moves!
Block moves are fundamental mutations of DNA-molecules, so the block move distance can also be used for phylogenic estimates. The talk will review what is known about the problem and what we believe to be true. (Joint work with Kimmo Eriksson, KTH.)
May 6
David Ingerman (NYU)
Inverse boundary problems, arrangements of pseudo-lines and total positivity
Abstract: Let $\Gamma$ be a planar graph embedded in a closed disk. Each positive weight function $\gamma$ on the edges of $\Gamma$ induces a response map of the graph (the linear map from Dirichlet to Neumann boundary data of $\gamma$-harmonic functions.) We will consider inverse boundary problems of obtaining information about the weighted graph from the response map. Our motivation for the study of these problems comes from their continuous PDE analogs (and originally from oil production industry). Surprisingly the answers turn out to be combinatorial in nature. For example: Every weighted graph is determined by its response matrix up to simple Reidemeister type transformations. The quotient of the weighted graphs by the transformations is essentially the set of circular permutations. There is a natural one-to-one correspondence between the graphs for which the inverse problem has unique solution and the arrangements of pseudo-lines on the plane. The response matrices are completely characterized by their total positivity property (sign conditions on determinants of minors.)
May 8
Christian Lenart (MIT)
Combinatorial Aspects of the K-theory of flag varieties
Abstract: In this talk we present some results concerning Grothendieck polynomials, which are representatives for the classes corresponding to Schubert varieties in the K-theory of the flag variety. Grothendieck polynomials are nonhomogeneous polynomials whose lowest homogeneous component is the Schubert polynomial indexed by the same permutation; hence they offer more information about the geometry of the flag variety than Schubert polynomials. The first part of the talk is devoted to Grothendieck polynomials corresponding to Grassmannian permutations; we discuss their expansion in the basis of Schur polynomials and a Pieri rule. In the second part of the talk, we sketch the proof of a conjecture of A. Lascoux concerning the expansion of an arbitrary Grothendieck polynomial in the basis of Schubert polynomials, and present a combinatorial interpretation for the coefficients of this expansion. The proof is based on certain noncommutative analogs of Schubert polynomials, for which we prove a Pieri rule and a Cauchy identity, thus extending the work of S. Fomin and C. Greene on noncommutative Schur functions.
May 8
Jim Propp (MIT)
Diabolo tilings of fortresses
Abstract: Diabolo tilings of fortresses are combinatorial objects that share some features with domino tilings of Aztec diamonds, rhombus tilings of hexagons, and alternating sign matrices, but that also exhibit novel phenomena that are not yet entirely understood. Here is a diabolo tiling of a fortress of order 7:
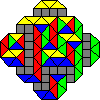
After defining these tilings, I will present Mihai Ciucu's simple proof of Bo-Yin Yang's formula for the number of diabolo tilings of the fortress of order n, using the graph-theoretic method of "urban renewal". Then I will show how extensions of urban renewal allow one to efficiently sample uniformly from the set of such tilings, and to encode statistical properties of random tilings via generating functions.
These techniques suggest, and should eventually allow us to prove, that in addition to (homogeneous) "frozen regions" and a (non-homogeneous) "liquid region", diabolo tilings of fortresses also exhibit "gaseous" behavior in the center of the tiling, as seen in http://www-math.mit.edu/~propp/hidden/fort200.ps.gz (a random diabolo tiling of a fortress of order 200) and http://www-math.mit.edu/~propp/hidden/fort300.5.ps.gz (a color-plot of the local statistics for the ensemble of random diabolo tilings of a fortress of order 300). Other displays used in this talk can be found at http://www-math.mit.edu/~propp/diabolo.ps.gz.
This is joint work with Mihai Ciucu, Henry Cohn, Rick Kenyon, David Wilson, and the undergraduate members of the Tilings Research Group. The talk presupposes no knowledge of tiling theory or statistical mechanics.
Note that the talk will take place in room 2-131 (not the usual meeting place for the seminar).