This test is closed book. You are not permitted to bring any books, notes
or such material with you. You may use theorems, lemmas and propositions
from the book or from class.
Note that most of the solutions are relatively short - this is likely to
be the case in the final as well!
- If
![$ f_n\in L^2([0,1])$](img416.png) is a convergent sequence, with respect to the
is a convergent sequence, with respect to the
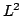 norm show that there is a subsequence which converges
pointwise almost everywhere.
norm show that there is a subsequence which converges
pointwise almost everywhere.
Solution:- Since ![$ [0,1]$](img319.png) has finite measure we know that
has finite measure we know that
![$ L^2([0,1])\hookrightarrow L^1([0,1])$](img418.png) and in fact
and in fact
Now, from results in class we know that any sequence which converges in
![$ L^1([0,1])$](img420.png) has a subsequence which converges almost everywhere. It
follows form the estimate above that if
has a subsequence which converges almost everywhere. It
follows form the estimate above that if 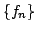 converges in
converges in 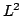 it
converges in
it
converges in 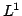 and hence has a subsequence which converges almost
everywhere in
and hence has a subsequence which converges almost
everywhere in ![$ [0,1].$](img403.png)
- Suppose that
![$ f\in L^2([-\pi,\pi])$](img407.png) has Fourier coefficients
has Fourier coefficients 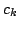 satisfying
satisfying
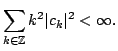 |
(44) |
Show that 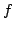 is continuous on
is continuous on
![$ [-\pi,\pi].$](img423.png)
Solution:- Since
![$ f\in L^2([0,1])$](img424.png) we know that its Fourier series
converges to
we know that its Fourier series
converges to 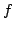 in
in
![$ L^2([-\pi,\pi])$](img311.png)
Now, consider the Fourier series itself, under the assumption (1).
If 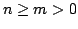 then
where we have used Schwarz' inequality. From the assumed convergence it
follows that the right hand side is arbitrarily small if
then
where we have used Schwarz' inequality. From the assumed convergence it
follows that the right hand side is arbitrarily small if 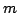 is large
enough. That is, the Fourier series itself is Cauchy in the uniform norm,
hence uniformly convergent. It follows that the limit of this series is
continuous and that it is a representative of
is large
enough. That is, the Fourier series itself is Cauchy in the uniform norm,
hence uniformly convergent. It follows that the limit of this series is
continuous and that it is a representative of 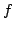 (this is what continuity
of
(this is what continuity
of 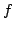 means, it has a continuous representative).
means, it has a continuous representative).
- Let
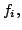
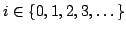 be the sequence obtained by
orthonormalization (the Gramm-Schmid process) of
be the sequence obtained by
orthonormalization (the Gramm-Schmid process) of
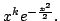 Show that for each
Show that for each 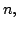 the Fourier transform
the Fourier transform
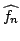 is linearly
dependent on
is linearly
dependent on
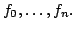
Solution:- The Gram-Schmid process replaces the
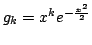 by
by
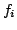 where each
where each 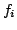 is a linear combination of the
is a linear combination of the 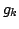 for
for 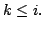 Thus it is enough to show that
Thus it is enough to show that 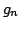 itself is linearly dependent on the
Fourier transforms
itself is linearly dependent on the
Fourier transforms
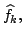
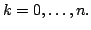 Now, we also know that
Now, we also know that
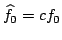 for some non-zero constant
for some non-zero constant 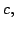 so the statement is
true for
so the statement is
true for 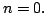 We can proceed by induction, assuming that we have already
shown that the statement is true for
We can proceed by induction, assuming that we have already
shown that the statement is true for 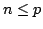 and then just prove it for
and then just prove it for
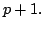 In fact the Fourier transform satisfies
In fact the Fourier transform satisfies
Again by induction we therefore know (in fact we showed in class) that
where 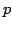 is a polynomial of degree at most
is a polynomial of degree at most 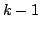 and
and
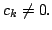 Thus by
induction we see that the Fourier transform of
Thus by
induction we see that the Fourier transform of 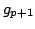 is a linear
combination of the
is a linear
combination of the 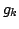 for
for
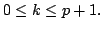
- Show that if
![$ f:[-\pi,\pi]\longrightarrow \mathbb{C}$](img411.png) is a bounded
measurable function which satisfies
is a bounded
measurable function which satisfies
![$ \int_{[-\pi,\pi]}x^{2k}f(x)dx=0$](img454.png) for
all non-negative integers
for
all non-negative integers
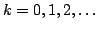 then there is an odd function
then there is an odd function
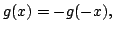 such that
such that 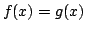 for almost all
for almost all
![$ x\in[-\pi,\pi].$](img410.png)
Solved:- Since 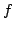 is bounded and measurable, it is in
is bounded and measurable, it is in
![$ L^2([-\pi,\pi]).$](img195.png) Consider the function
Consider the function
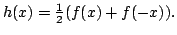 This is even and in
This is even and in
![$ L^2([-\pi,\pi]).$](img195.png) Moreover it satisfies
Moreover it satisfies
For even powers this follows from the assumption on 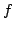 since
On the other hand for odd powers
since
On the other hand for odd powers
Now, we know that polynomials are dense in
![$ L^2([-\pi,\pi])$](img311.png) so we can
choose a sequence
so we can
choose a sequence
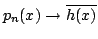 in
in
![$ L^2([-\pi,\pi]).$](img195.png) Thus it
follows that
Thus it
follows that
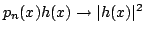 in
in
![$ L^1([-\pi,\pi])$](img463.png) and hence that
and hence that
![$\displaystyle \int_{[-\pi,\pi]}\vert h(x)\vert^2dx=0\Longrightarrow h=0$](img464.png)
almost everywhere.
That 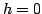 almost everywhere implies that
where
almost everywhere implies that
where  is an odd function.
is an odd function.
Richard B. Melrose
2004-05-24
![]() has finite measure we know that
has finite measure we know that
![]() and in fact
and in fact
![]() we know that its Fourier series
converges to
we know that its Fourier series
converges to ![]() in
in
![]()
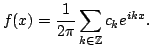
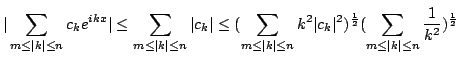
![]() by
by
![]() where each
where each ![]() is a linear combination of the
is a linear combination of the ![]() for
for ![]() Thus it is enough to show that
Thus it is enough to show that ![]() itself is linearly dependent on the
Fourier transforms
itself is linearly dependent on the
Fourier transforms
![]()
![]() Now, we also know that
Now, we also know that
![]() for some non-zero constant
for some non-zero constant ![]() so the statement is
true for
so the statement is
true for ![]() We can proceed by induction, assuming that we have already
shown that the statement is true for
We can proceed by induction, assuming that we have already
shown that the statement is true for ![]() and then just prove it for
and then just prove it for
![]() In fact the Fourier transform satisfies
In fact the Fourier transform satisfies
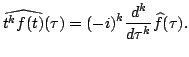
![]() is bounded and measurable, it is in
is bounded and measurable, it is in
![]() Consider the function
Consider the function
![]() This is even and in
This is even and in
![]() Moreover it satisfies
Moreover it satisfies
![$\displaystyle \int_{[-\pi,\pi]} x^kh(x)dx=0\ \forall\ k=0,1,\dots.
$](img457.png)
![$\displaystyle \int_{[-\pi,\pi]} x^{2k}f(-x)dx=\int_{[-\pi,\pi]} x^{2k}f(x)dx.
$](img458.png)
![$\displaystyle \int_{[-\pi,\pi]} x^{2k+1}f(-x)dx=-\int_{[-\pi,\pi]} x^{2k+1}f(x)dx$](img459.png)
![$\displaystyle \Longrightarrow \int_{[-\pi,\pi]} x^{2k+1}h(x)dx=0.$](img460.png)
![$\displaystyle \int_{[-\pi,\pi]}\vert h(x)\vert^2dx=0\Longrightarrow h=0$](img464.png) almost everywhere.
almost everywhere.