Next: The final Up: 18.103, Spring 2004 Previous: Test 2 with solutions
This exam is closed book, no books, papers or recording devices permitted. You may use theorems from class, or the book, provided you can recall them correctly.
Suppose
![]() and
and
![]() for all simple
measurable functions
for all simple
measurable functions ![]() on
on ![]() Show thatt
Show thatt ![]() almost everywhere with
respect to Lebesgue measure.
almost everywhere with
respect to Lebesgue measure.
Ans. Take ![]() to be the characteristic function of the measureable set
to be the characteristic function of the measureable set
![]() Then
Then
![]() implies that
implies that ![]() a.e. - the same argument works for
a.e. - the same argument works for ![]() so
so ![]() a.e.
a.e.
Suppose ![]() is a compact operator on a Hilbert space
is a compact operator on a Hilbert space ![]() and that
and that ![]() has no positive eigenvalues, show that
has no positive eigenvalues, show that ![]()
Ans. Since ![]() is compact and selfadjoint there is a complete
orthonormal basis of its eigenvectors. All the eigenvectors must be
non-negative, since
is compact and selfadjoint there is a complete
orthonormal basis of its eigenvectors. All the eigenvectors must be
non-negative, since
![]() imples
imples
![]() So, if there are no positive eigenvalues they must all be zero. Thus
So, if there are no positive eigenvalues they must all be zero. Thus
![]() for all
for all ![]() implies
implies ![]() for all
for all ![]() so
so ![]()
Give an example of a function
![]() which is continuous
but is such that its Fourier transform
which is continuous
but is such that its Fourier transform
![]()
Ans. For any ![]() it is easy to find a non-negative continuous function,
it is easy to find a non-negative continuous function, ![]() with
maximum
with
maximum ![]() supported in
supported in
![]() The integral of its square is
then less than
The integral of its square is
then less than ![]() Consider the function
Consider the function
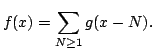
Suppose
![]() and there exists
and there exists
![]() such
that
such
that
Ans. Plug ![]() into the identity for each
into the identity for each
![]() and you
find that the Fourier coefficients
and you
find that the Fourier coefficients ![]() of
of ![]() satisfy
satisfy ![]() where
where
![]() are the Fourier coefficients of
are the Fourier coefficients of
![]() Thus
Thus
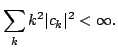
Suppose
![]() has Fourier transform satisfying
has Fourier transform satisfying
![]() in
in ![]() Show that there exists
Show that there exists
![]() such that
such that
![]() for all
for all
![]()
Ans. The function
![]() in
in
![]()
![]() in
in
![]() is in
is in
![]() and satisfies
and satisfies
![]() Thus if
Thus if ![]() is the inverse Fourier transform
of
is the inverse Fourier transform
of ![]() it is in
it is in
![]() and satisfies
and satisfies
![]()
Show that there is no element of
![]() satisfying
satisfying
Ans. This stops the Fourier coefficietns of ![]() from vanishing at
from vanishing at ![]()
Suppose
![]() had Fourier coefficients
had Fourier coefficients ![]()
![]() satisfying
satisfying
Ans. The given condition implies he uniform convergence of the (formal)
Fourier series for ![]() So
So ![]() has a continuous first
derivative. Integration by parts is then justified in the given identity so
we can take
has a continuous first
derivative. Integration by parts is then justified in the given identity so
we can take
![]()
If
![]() show that
show that
Ans. Change variables to shift the integral to
![]() (or use Fourier
series on
(or use Fourier
series on ![]() by setting
by setting
![]() The
The
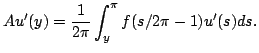
Show that there is an infinite orthonormal sequence
![]() with each element satifying
with each element satifying
Ans. The eigenfunctions of the harmonic oscillator.
Richard B. Melrose 2004-05-24