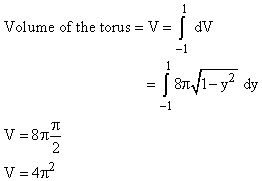Introduction

Introduction

The method of washers involves slicing the figure into washer shaped slices and integrating over these. It is highlyappropriate for computing the volume of a torus.

Rotate the circle

By rotating the circle around the y-axis, we  generate a solid of revolution called a torus whose volume can be calculated using the washer method.

Washer method

We revolve around the y-axis a thin horizontal strip of height dy and width R - r.

This generates a disk with a hole in it (a washer) whose volume is dV.

R = right hand "x" value of the circle =

r = right hand "x" value of the circle =

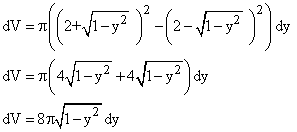
Volume of the torus

We get the volume of the torus by filling it with a very large number of very thin washers, that is by integrating dV from y = -1 to y = 1.