18.366 Random Walks and Diffusion

Various mathematical aspects of (discrete) random walks and (continuum) diffusion are developed in the context of applications in physics, chemistry, biology, and economics.

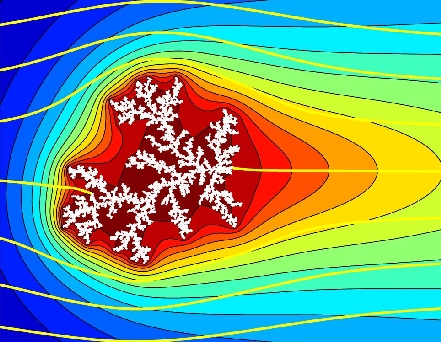
Course Description: Mathematical modeling of diffusion phenomena: central limit theorems, the continuum limit, first passage, persistence, continuous-time random walks, Levy flights, fractional calculus, random environments, advection-diffusion, nonlinear diffusion, free-boundary problems. Applications may include polymers, disordered media, turbulence, diffusion-limited aggregation, granular flow, and derivative securities.

Time and Place: TR 11-12:30, Room 2-147, MIT.

Prerequisite: 18.305 or permission of the instructor. A basic understanding of probability, partial differential equations, transforms, complex variables, asymptotic analysis, and computer programming would be helpful, but an ambitious student could take the class to learn some of these topics. Interdisciplinary registration is encouraged.

Textbooks

• Lecture notes from 18.325 (spring 2001).
• Sidney Redner, A Guide to First Passage Processes (Cambridge, 2001).

• Barry Hughes, Random Walks and Random Environments, Volume 1 (Oxford, 1996).
• John Crank, The Mathematics of Diffusion, 2nd edition (Oxford, 1975).
• D. Ben-Avraham and S. Havlin, Diffusion and Reactions in Fractals and Disordered Systems (Cambridge, 2000).
• Jean-Philippe Bouchaud and Marc Potters, Theory of Financial Risks (Cambridge, 2000).

bazant@mit.edu