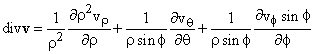The gradient of a scalar and divergence and curl of a vector have a simple form in rectilinear coordinates. This form is maintained if you move the origin or rotate the coordinates, but still use rectilinear coordinates.
Their forms change, however, under if you choose arbitrary coordinates, and they look quite different even in polar coordinates in the plane, and in cylindric and spherical coordinates in three dimensions.
We will derive the form of the divergence and curl in an arbitrary orthogonal coordinate systems by application of Stokes' theorem and the divergence theorem.
The character of a coordinate system that affects the form of these objects is encapsulated in the expression for distance in the coordinate system.
In rectilinear coordinates distance is described by the Pythagorian Theorem:  ds² = dx² + dy² + dz².
In a general orthogonal coordinate system, with variables w₁ , w₂ and w₃, distance can take on the more general form
ds² = u₁²dw₁² + u₂²dw₂² + u₃²dw₃², where the u's are each functions of the variables.
Thus,

In polar coordinates with w₁ = r and w₂ = q, we have

u₁ =1 and u₂ = r: ds² = dr² + r²d²

In spherical coordinates with w₁ = , w₃ = and w₂ =, and r = rsin, we have

u₁ =1, u₃ = r =sin and u₂=: ds² = d² + r²d² + ²d

In cylindric coordinates, we have

ds² = dr² + r²d² + dz²

We now apply the divergence theorem to a little rectangular box of space around the point r oriented with sides parallel to the directions of w₁ , w₂, and w₃, so that the  the coordinates change by dw₁, dw₂ and dw₃ in it. We make these quantities so small that div v is essentially constant inside it, and v is essentially constant on it boundaries.
We get:

(div v(r))V = d(A₁v₁(r)) + d(A₂v₂(r)) + d(A₃v₃(r))

where A_i is the area of the part of the boundary of our box on which w_i is constant, and V is the volume of the box.
We can differentiate to get

and  observe that

and V = u₁u₂u₃dw₁dw₂dw₃

Substituting these facts into the last equation  and dividing by V gives us

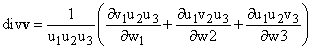
The key observation here is that both v_i and A_i can change across the box, so that one must differentiate the product v_i A_i and not just v_i .

In two dimensions, there is no w₃ and the same equation holds without any last term and with u₃ =1.

Thus, in polar coordinates, we get:

In spherical coordinates we find

Exercises