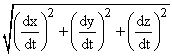Suppose we have a path P in two dimensions from x₀ y₀ to (x _f , y _f) defined by an equation:

y - f(x) = 0

or more generally

g(x, y) = 0

Suppose further we seek to evaluate a circulation measure integral along this path. We do this by reducing it to an ordinary  integral with a modified integrand, and then integrating it.

If we define the vector w by , the integral

becomes the ordinary integral

Proof

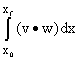
We have assumed here that the variable x changes monotonically along the path (it keeps increasing or decreasing). Otherwise you have to break the integral up into pieces on each of which x is monotone, if you want to use x as your variable of integration.

More generally, if you use a parameter t to describe your path, the relevant vector w is given by

w and one integrates vw dt.

If you want to integrate using length measure, as you would to compute arc-length along the path, then you integrate the magnitude of w, 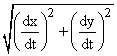times the integrand f, instead of vw. This gives exactly the expressions for arc length encountered in single variable calculus.

In three dimensions, the only difference, given parameter t, is that w is given by

and its magnitude is