In three dimensions, a single equation typically can determine only one coordinate given the other two. It therefore usually defines a surface and not a curve. Thus x² + y² = 4 defines an infinite cylindric surface or tube of radius 2 with the origin on its axis of symmetry.To describe a curve or path by equations you typically need two of them. On the other hand, the parametric description works equally well in two or three dimensions; the only difference is in three dimensions you must describe the third coordinate, z,  in terms of the parameter as well as x and y.
A surface in three dimensions is often presented by a defining equation; one can also describe it by parameters, but one requires two of them: varying one parameter can only produce a one dimensional figure, some sort of curve.Thus a circular tube of radius 2 around the origin stretching from z = -1 to z = 1 can be described by the parameters z and in the obvious way. The surface of a sphere of radius a with the origin as center can be described by the angle parameters of spherical coordinates, and :

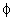r = x i + y j + z k,

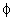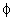x = a sincos, y = a coscos, z = acos,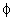

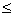
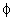
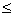
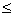
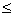0 , 0 2.