Home | 18.022 | Chapter 4

Tools    Index    Up    Previous    Next

4.2 Maxima and Minima

Suppose we have a function f (x, y) or f (x, y, z) defined in some domain, and seek a global maximum for it, in that domain.We may do so as in ordinary calculus, by finding critical points in the interior of our domain and comparing behavior at them with that at its boundaries.
The condition for a point r' to be critical for f is that all directional derivatives of f vanish at r = r'. This is the statement that f is the zero vector, and all of its components vanish for (x, y, z) = (x', y', z'):

The connection between critical points and maxima and minima is more complicated here than in one dimension, because the behaviors of quadratic functions in two or more dimensions are more complicated than they are in one dimension. In any case a well behaved function looks like a quadratic function at a critical point unless all its second derivatives also vanish there.
In one dimension all quadratics look the same except for scale and sign; the sign of the second derivative  determines whether the critical point is a maximum, minimum or inflection point. In higher dimensions, on the other hand, we can have a saddle point as well.

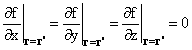
Consider quadratics critical at the origin in two dimensions:  they can behave like any of :

x2 + y2 which has a minimum there.

-2x2 - 3y2 which has a maximum there.

x2 - y2 which has a saddle point.                                   

xy which has a saddle point.

10xy - x2- y2 which has a saddle point.

The coefficients of the quadratic that f resembles at r' are determined by the second partial derivatives of f at r'. In order for the critical point to be a minimum, the second partials with respect to x and y must both be positive, and they must be large enough to dominate the xy term corresponding to the cross partial .
The actual condition is the familiar discriminant, b2 -4ac, of the quadratic must be negative, which means, in terms of derivatives, that the square of the cross partial is less than the product of the other two:

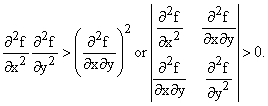
In three dimensions a critical point will be a minimum when the "diagonal partials" are positive, the two dimensional condition holds for all pairs of variables (x, y), (x, z) and (y ,z), and the three dimensional determinant of the second partial derivatives is also positive.

We get a maximum when all diagonal second derivatives are negative,  as is the three by three determinant of second partials, and the two by two determinants are all positive. (You can see this by changing the sign of f and applying the minimum conditions to -f. The two by two conditions are unaffected by the sign change.)