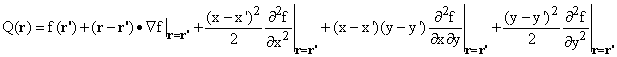4.1 Linear and Quadratic Approximations

4.1.1 Introduction

A differentiable function f is one that resembles a linear function at close range. The linear approximation to f at a point r' is the linear function it resembles there. If f has second derivatives ar r' the quadratic function having the same second derivatives is the quadratic approximation to it at r'.
In one dimension the graph of a function against the independent variable is a curve, and the linear approximation to it is the function whose graph is the tangent line to it at r'.
In two dimensions, the graph of f against the two independent variables, is a surface, and the linear approximation to it at r' is the plane tangent to that surface at r'.

4.1.2 How do we find the linear approximation to f at r' ?

In one dimension the linear function L, L = a(x - x') + b is determined by the conditions that

We get

In higher dimension, if we write the linear approximation function as L:

L = a₁(x-x') + a₂(y - y') + a₃(z - z') + b = a(r - r') + b

we obtain

To compute the quadratic approximation, you compute the second partial derivatives and insert quadratic terms that give the same derivatives.

4.1.3 How do we use the linear approximation?

The obvious use of the linear approximation is in estimating the value of a function at r = r" knowing its value at r' and its gradient there.
We get

4.1.4 How do we use the quadratic approximation?

The quadratic approximation which we write out in detail in two dimensions, is of great use in determining the nature of a critical point at r', and can be useful in approximating f when the linear approximation is insufficiently accurate.
We denote the quadratic approximating function to f at r' by Q.
We then have