 .
.
|
||
|
|
||
|
The method used here, that of cylindric shells, is particularly well adapted to computation of Moments of Inertia of a mass distribution.
Moment of inertia is defined with respect to an axis. Each bit of mass contributes to the moment of inertia an amount given by its mass times the square of its distance to that axis. If the volume in the example here were filled by an object with uniform density, the only change necessary to compute moment of inertia about the y axis here instead of volume (or mass) is an additional factor of x2.
You can verify that this will only change the factor of ![]() in the answer to
in the answer to ![]() . The moment of inertia of a uniform density body of mass M in the volume above
the y axis is therefore given by
. The moment of inertia of a uniform density body of mass M in the volume above
the y axis is therefore given by 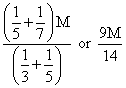 .
.