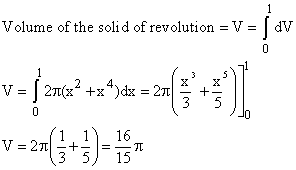Calculate the volume generate by rotating the area A: around the y-axis.

Comment

Rotate the area

By rotating the area A, we generate a solid of revolution whose volume can be calculated using the shell method.

Shell method

We revolve around the y-axis a thin vertical strip of height y and width dx.

This generates a thin-walled cylindrical shell whose volume is dV.

dV is the area of the inner surface (2pxy) times the thickness of the wall (dx).

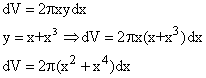
Volume of the torus

We get the volume of the solid of revolution by filling it with a very large number of very thin concentric shells, that is by integrating dV from 0 to 1.