|
||
|
|
||
|
We can approximate an integral by choosing n, iding the integration interval into n parts and using a Riemann sum as our approximation.
Let Ln be the result of computing the left Riemann sum in this way,
and Rn be the right Riemann sum. The "trapezoid rule" is
![]() .
.
Here are explicit formulae for these approximate sums:
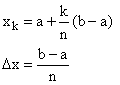
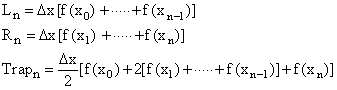
Simpson's rule works only for n even and gives different weight to the f(xk) depending on the evenness or oddness of k:
![]()
![]()