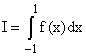using Simpson's rule with n = 2.
|
||
|
|
||
|
Why these weigths? Because they are exactly correct even for n = 2 if f is a cubic polynomial.
Suppose: f(x) = a0 + a1x + a2x2 + a3x3
Calculate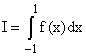
using Simpson's rule with n = 2.
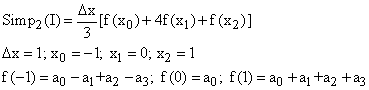
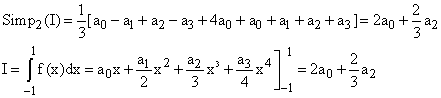
Thus Simpson's rule, with n = 2 is the exact integral on any cubic!
As a consequence of this fact, if we ide our interval into pieces in each of which f is not far from a cubic, Simpson's rule will be very accurate.