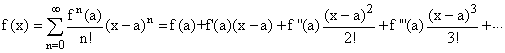
|
|
||
|
|
||
|
Functions made up by combining constants, using addition, substraction, multiplication, ision, substitution, have these wonderful properties:
1.They are defined everywhere on the real line except possibly on those points at whichthe denominator vanishes.
2.The values of such a function on any tiny interval, or the values of all its derivatives at any single point where they all exist, determine its value for every x on the real line and in the complex plane.
If for one point a all the f n(a) exist, then the formula called
the Taylor expansion of f at a,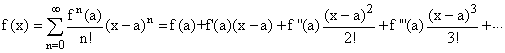
can be used to define f(x) for almost all x.
This series formula has all its derivatives arranged to agree with those of f at a. We can approximate f near a by taking the first few terms in this series, the more taken the better the approximation.