|
||
|
|
||
|
A satellite 1000 km above the earth is used to measure r, which is how far objects on earth are from directly below it, by timing reflections of radio signals. How fast must its clock be to measure within an accuracy of 1 km?
We ignore the curvature of the earth here for simplicity
The signal travel a distance 2d and hence take a time 2d / c where c is the velocity of radio signals which is 3.105 km / s.
d2 = 10002 + r2, so that ![]()
The time difference for a given change Dr in r obeys
![]()
We therefore get
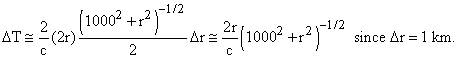
We study the function ![]() ,
y(r) being the accuracy needed to measure distance 1 km as a function of r distance
from pole.
,
y(r) being the accuracy needed to measure distance 1 km as a function of r distance
from pole.
![]()
Step 1
No singular points
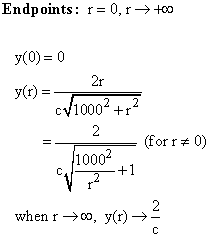
Step 2
Calculation of y'
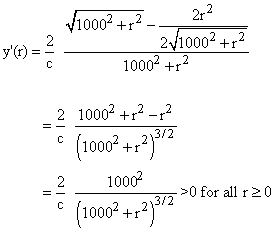
There is no critical point.
Conclusion
As we can see on the graph most measurements can be done with an accuracy of 10-7 (quartz clock).
A cesium clock (accuracy 10-11s) is needed only for very small values of r.