Philippe Rigollet

Philippe Rigollet is the Cecil and Ida Green Distinguished Professor of Mathematics. His research interests span a wide range of mathematical topics, particularly those emerging from the fields of statistics, data science, and artificial intelligence. Currently, he focuses on statistical optimal transport and the mathematical foundations of Transformers.

Affiliations

Mathematics

IDSS

LIDS

Broad Institute

Academic Positions

Professor

MIT, Mathematics, 2020 -

Associate Professor

MIT, Mathematics, 2016 - 20

Assistant Professor

MIT, Mathematics, 2015 - 16

Assistant Professor

Princeton, ORFE, 2008 - 14

Postdoc

Georgia Tech, Mathematics, 2007 - 08

Education & Training

Ph.D. in Mathematics

Univ. of Paris 6 (now Sorbonne Univ.) - 2006

M. Sc. in Statistics & Actuarial Science

ISUP - 2003

B. Sc. in Applied Mathematics

Univ. of Paris 6 (now Sorbonne Univ.) - 2002

Selected Awards

Frank E. Perkins Award

2023

The Frank E. Perkins Award for Excellence in Graduate Advising is given each year to a professor from each school who has served as an excellent advisor and mentor for graduate students. The award is named in honor of Frank E. Perkins, Dean of the Graduate School from 1983-95.

Medallion lecture. Joint Statistical Meetings.

2021

Lecture on "Statistical Optimal Transport". Watch video here .

Elected IMS Fellow.

2021

For outstanding contributions to the analysis of statistical versus computational trade-offs, to the theory of aggregation, and to statistical optimal transport.

Invited lecturer. St Flour Probability Summer School.

2019

Lectures on "Statistical Optimal Transport". More information here. Lectures notes will be available Fall 23.

Best Paper Award.

2013

Berthet and Rigollet received "best paper award" at the Conference On Learning Theory (COLT) for their paper "Complexity Theoretic Lower Bounds for Sparse Principal Component Detection". In this work, they show that employing computationally efficient statistical methods in the context of sparse principal component analysis leads to an ineluctable deterioration of statistical performance, regardless of the efficient method employed. In particular, their paper draw new connections between statistical learning and computational complexity. An extended version of the paper is available here.

NSF CAREER Award.

2011

Large Scale Stochastic Optimization and Statistics..

Featured Work

Transformers and Self-Attention dynamics

ArXiv [2305.05465][2312.10794]

Our group recently initiated a line of work where we aim to develop a mathematical perspective on transformers by viewing them as interacting particle systems. As in neuralODEs, we view (self-attention) as velocity fields that evolve particles (token) towards a useful embedding. Our initial work has largely focused on shedding light on the clustering behavior of this system of interacting particles. Even in a very stylized model, many intriguiging mathematical questions arise.

Wasserstein gradient flows

YouTube EBA0NyY4Myc

This talk gives an overview of our recent work on applications of Wasserstein gradient flows to problems arising in statistics and machine learning. The Wasserstein geometry and its extensions (notably Wasserstein-Fisher-Rao) provide a toolbox to develop particle-based optimization algorithms over probability measures. These ideas have been implememented in several examples such as variational inference and nonparametric maximum likelihood estimation.

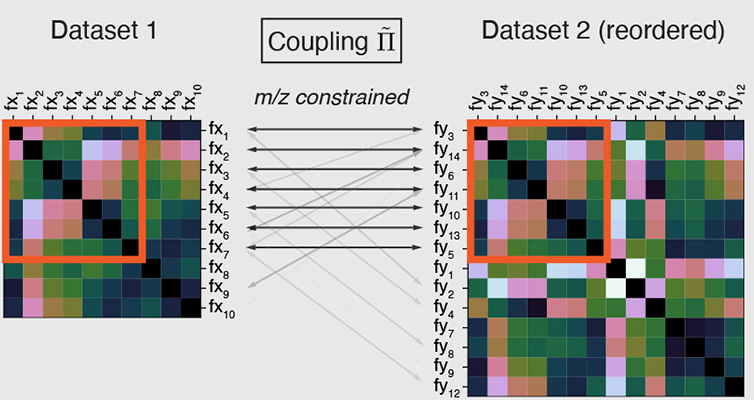
Biological applications

ArXiv 2306.03218

Our group explores applications of novel mathematical ideas to biological data, including genomics data in collaboration with the Eric and Wendy Schmidt Center at the Broad Institute. Our past work has focused on using optimal transport and the Gromov-Wasserstein framework to combine multiple sources of data and we are currently exploring new tools for new applications, including spatial transcriptomics.

Research Group

Aleksandr Zimin

Ph.D Student

Anya Katsevich

NSF Postdoc

Enric Boix

Postdoc

Max Daniels

Ph.D Student

Mohammad Reza Karimi

Instructor in Applied Math

Nicholas Nelsen

NSF Postdoc

Shi Chen

Instructor in Applied Math

Tudor Manole

Wiener Postdoc

Yajit Jain

EWSC Postdoc

Zhengjiang Lin

C.L.E Moore Instructor

Ziang Chen

Instructor in Applied Math

Openings

Interested in joining our group?

I cannot answer direct requests but you are encouraged to explore the various oppotunites at both the graduate and the postdoc levels. Make sure to check this page regularly, especially in the Fall.

Instructor

Applied Mathematics

Competitive 3yr postdoc with higher salary and teaching duties

Postdoc

Eric & Wendy Schmidt center

I am looking for postdocs interested in exploring new connections between mathematical methods and biology, esp. genomics. The new Eric & Wendy Schmidt postdocs offers a perfect opportunity for such collaborations.

Wiener Fellowship

Statistics and Data Scence Center

The Wiener Fellowship is a competitive postdoc in the Statistics and Data Science Center at MIT. Laureates are expected to collaborate with several members of the center

Postdoc

School of Science

The School of Science's 3-year Postdoctoral Fellowship is aimed at scholars engaged in cross-disciplinary research.

Ph.D student

Mathematics department

This group admits Ph.D. students exclusively through the Mathematics department at MIT. Decisions are made at the departmental level rather than at the faculty level.

Current Funding

NSF CCF-2106377

Collaborative Research: CIF: Medium: Analysis and Geometry of Neural Dynamical Systems

NSF DMS-2022448

TRIPODS: Foundations of Data Science Institute

Contact

The best way to contact me is via email

View Email Address