There are many approaches to conventional Euclidian scattering theory. In this exposition an essentially microlocal view is adopted. Apart from its intrinsic interest this is intended as preparation for later generalization, to more complicated geometric settings. In fact, the treatment given here extends beyond the usual confines of scattering theory in that the spectral and scattering theory, at least the elementary part, is covered for the Laplacian associated to a `scattering metric' on any compact manifold with boundary.
By a scattering metric on a compact manifold with boundary, X, we shall mean a Riemann metric on the interior of X which can be brought to the form
where 
is a boundary defining function
and h is a smooth symmetric 2-tensor on X which is non-degenerate when
restricted to the boundary. Clearly the existence of x and h such that
(1) holds is only a limitation on the behaviour of the metric
near the boundary. Such a metric is asymptotically flat in the sense that
the Riemann curvature tensor extends smoothly up to the boundary and
vanishes there.
One virtue of scattering metrics is that they exist on any compact manifold
with boundary and in this sense the theory is universal. The prototypical
example is Euclidian space. Namely if 
is compactified to a
unit hemisphere by stereographic projection, as discussed in Section , then
the Euclidian metric takes the form (1) near the boundary.
A scattering metric is a, rather special, example of a metric on the
structure bundle of the Lie algebra 
where 
is
the Lie algebra of all smooth vector fields on X which are tangent to the
boundary. The space 
is a boundary-fibration structure
(which notion we do not define or use here) in the sense of daomwc,
with structure bundle
this is discussed in Section S.Sa. The basic approach taken here and
examined in some generality in daomwc is that the boundary-fibration
structure, in this case just 
should be thought of as a
geometry. This approach is based on the development of a calculus of
pseudodifferential operators, appropriate to the context and coming from
the geometry. This calculus can then be applied, much as the usual calculus
of pseudodifferential operators on a compact manifold without boundary can
be applied, to give regularity, and in particular propagation, results.
Here the `small calculus' of scattering pseudodifferential operators is
discussed and used to prove commutator estimates analogous to those found
in scattering theory on Euclidian space. In particular we give a variant of
Mourre's estimate (Mourre) in this setting. For the half-sphere,
this calculus reduces to one of the standard versions of
the global pseudodifferential calculus on 
via stereographic
projection.
In fact three examples of boundary-fibration structures occur here; they
can be recognized by the elliptic operators associated to each. Let 
be a coordinate defining the boundary (which is `at infinity') and let
be tangential coordinates. Then, with
and 
typical (invertible) elliptic
operators are
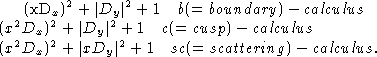
Although the cusp calculus is not discussed in detail here, it would be natural to do so since its use makes the regularity results of Section S.Src more precise. Whereas the scattering calculus is tempered, in the sense that it is locally contained in the Weyl calculus of Hörmander HoWC, this is not the case for either the boundary or cusp calculi.
The material below falls naturally into three parts, the contents of which are described in more detail below. In Section sS.SpS.WF the quantization of the Lie algebra of vector fields associated to the metric (1) is explained. The central sections, Section sS.PtpS.Lrp contain the main analytic results, concerning the behaviour of the limit of the resolvent of the Laplacian on the spectrum and leading in particular to the definition of the scattering operator. In the third part, consisting of the appendices, the direct and intrinsic approach to the quantization is outlined.
The properties of the scattering operator in this generality remain to be investigated. In the Euclidian context, the scattering operator (at fixed energy) as defined in Section S.So is of the form R+A, where R is the anitpodal reflection of the sphere and A is a smoothing operator. In the general case of a scattering metric the appropriate generalization is expected to be:
Comjecture The scattering operator associated to a scattering
metric is a Fourier integral operator with canonical relation the geodesic
flow, at time 
of the boundary metric.
This can be construed as the statement that, for a metric
(1), infinity always has width 
Other topics which remain to be treated include:
This is considerably more complicated than in
the Euclidian setting since it is influenced strongly by the eigenvalues of
the induced Laplacian on 
The central result proved below is that
the 
-outgoing solution to 
where
vanishes with all its derivatives at
and
has a complete asymptotic expansion with leading term
This result, well known in the Euclidian setting, can be viewed as either a
strong form of the Sommerfeld radiation condition or a weak form of b)
above. The space of square-integrable functions with respect to the metric
volume form is written here 
Then 
for 
Moreover if for any 
then 
and u
vanishes rapidly at The critical exponent 
is seen to
arise from the commutator formula in the calculus of scattering
pseudodifferential operators.
The structure of scattering differential operators is discussed in
Section S.Sa, after it is shown in Section S.Sp that stereographic
projection, i. e. radial compactification, of converts the
translation invariance to such a structure. The properties of the
Laplacian, acting on forms, associated to a metric (1), are
examined in Section S.SL. The calculus of pseudodifferential operators
obtained by quantization of the structure algebra is introduced in
Section S.SD by reduction to and many of its properties are
described in Section S.PC; although full proof are not given. Further
discussion is relegated to
Appendix A.Sc. In Section S.RF the properties of the calculus are
used to show that the resolvent family for the Laplacian of (1)
is holomorphic in 
with values in the calculus. The
wavefront set associated to the scattering calculus, and a uniform version
of it, is investigated in Section S.WF; this language is used as a
convenient way to state microlocal estimates.
The first such estimates, reducing to Hörmander's propagation theorem for
operators of real-principal type, are given in Section S.Ptp. The more
subtle estimates, again proved by the positive-commutator method, around
the radial surfaces for the operator 
are given in
Section S.Rs. These are the main estimates used in the subsequent
analysis and amount to a version in this context of Mourre's estimate for
the N-body problem. In Section S.Aoee these basic estimates, together
with a unique continuation theorem, or Aronszajn-Cordes type, proved by
Hörmander (HoUC), show the absence of 
eigenfunctions for the
Laplacian. Various forms of the Sommerfeld radiation condition are
discussed in Section S.Src and the asymptotic expansion of
-outgoing solutions is deduced in Section S.Ae. The boundary
pairing for asymptotic data in Section S.Bp is used in Section S.Lap to
prove the limiting absorption principle, i. e. to examine the
limit of the resolvent as the parameter approaches the spectrum. Finally in
Section S.So these results are used to define the scattering operator for
the Laplacian. In Section S.Lrp the minor modifications needed to treat
long-range potentials are described.
The discussion below is intended to provide a bridge between the traditional methods of Euclidian scattering theory, which depends ultimately on the explicit inversion of the Euclidian Laplacian, and the more geometric problems encountered in the analysis of the Laplacian on complete Riemannian manifolds with uniform degeneracy at infinity, as typified by a metric singular at the boundary of a compact manifold with boundary. Indeed these scattering metrics form just such a class, but there are others of interest. Although all the results proved here are well known in the Euclidian setting we give proofs in this wider context. It is anticipated that the methods used here can be further generalized to give a unified treatment of the N-body problem and classes of singular metrics on manifolds with corners. For a recent discussion of the N-body problem see Yafaev.