Next: Solutions to Homework 7 Up: Solutions Previous: Solutions to Problem set
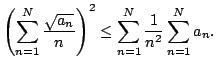
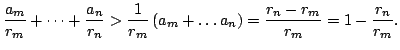 is not Cauchy
since the right side tends to
is not Cauchy
since the right side tends to
(b) Using the identity
![]() and the fact that
and the fact that ![]() is strictly decreasing, we conclude that
is strictly decreasing, we conclude that
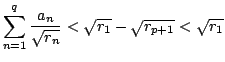 that
that
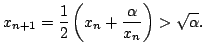 also follows that
also follows that
(b)Defining
![]() we find that
we find that
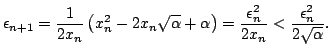 where
where
(c) If 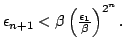 and
and ![]() then
then
![]() so
so
![]()
![]() and
and
![]() Since
Since ![]()
![]() and
and
![]()
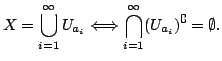 such that for
such that for
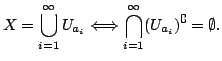 such that
such that Richard B. Melrose 2004-05-18