Homework

From now on will be due on Tuesdays - so that it can be graded by the following Thursday. For the next week I will accept homework in my office until 12 on Wednesday. To be put in a bin in 2-108 before Noon - there will be a box somewhere just inside the door.

1. due February 5: Rudin Chapter 1, Problems 1,3,5.
   1. [Exercise 1] If $s$ and $r\not=0$ are rational then so are $s+r,$ $-r,$ $1/r$ and $sr$ (since the rationals form a field). So if $r$ is rational and $x$ is real, then $x+r$ rational implies $(x+r)-r=x$ is rational. An irrational number is just a non-rational real number, so conversely if $x$ is irrational then $x+t$ must be irrational. Similarly if $rx$ is rational then so is $(xr)/r=x;$ thus if $x$ is irrational then so is $rx.$
   2. [Exercise 3]

      (a)

      If $x\not=0$ then $x^{-1}$ exists and if $xy=xz$ then

      $$y=(x^{-1}x)y=x^{-1}(xy)=x^{-1}(xz)=(x^{-1}x)z=z$$

      using first (M5) then (M2), (M3), the given condition, (M3) and (M5).

      (b)

      Is (a) with $z=1.$

      (c)

      Multiply by $x^{-1}$ so $x^{-1}=x^{-1}(xy)=(x^{-1}x)y=1y=y$ using associativity and definition of inverse.

      (d)

      The identity for $x^{-1}=1/x,$ $x\cdot x^{-1}$ gives by commutativity $x^{-1}\cdot x=1$ which means $1/(1/x)=x$ by the uniqueness of inverses.

   3. [Exercise 5] If $A$ is a set of real numbers which is bounded below then $\inf A$ is by definition a lower bound, i.e. $\inf A\le a$ for all $a\in A$ and if $\inf A\ge b$ for any other lower bound $b.$ We already know that if it exists it is unique. Now if $A$ is bounded below then

      $$-A=\{-x;x\in A\}$$ (1)

      
      
      is bounded above. Indeed if $b\le x$ for all $x\in A$ then $-b\ge -x$ for all $x\in A$ which means $-b\ge y$ for all $y\in -A.$ Now, if $\sup(-A)$ is the least upper bound of $-A$ it follows that $-\sup(-A)$ is a lower bound for $A$ since

      $$x\in A\Longrightarrow -x\in -A\Longrightarrow \sup(-A)\ge -x\Longrightarrow -\sup(-A)\le x.$$

      
      
      As noted above, if $b$ is any lower bound for $A$ then $-b$ is an upper bound for $-A$ so $-b\ge\sup(-A)$ and $b\le-\sup(-A).$ This is the definition of $\inf A$ so

      $$\inf A=-\sup(-A).$$

      
      

2. due February 11: Rudin Chapter 1, Problems 8, 9, 10 and Chapter 2 Problems 2,3,4.
3. due February 18: Rudin Chapter 2, Problems 9a, 9b, 9c, 11.
4. due February 25: Rudin Chapter 2, Problems 10, 12, 16, 22, 23, 25.
5. due March 2: Rudin Chapter 2, Problems 19, 20, 21, 24, 26, 29.
6. due March 9: Rudin Chapter 3, Problems 2, 7, 12, 16, 20, 21 (you should add the missing assumption that $E_n\not=\emptyset$ for all $n).$
7. due March 30. Rudin Chapter 4, Problems 1, 4, 15.
8. due April 6. Rudin Chapter 4, Problems 14, 18, 21. Chapter 5, Problems 1, 3, 4.
9. due April 13. Rudin Chapter 5, Problems 15, 16, 22. Chapter 6, Problems 1, 5, 7.
10. Nothing due April 20.
11. due May 4. This is the last homework: Rudin Chapter 7, Problem 6, 9, 10, 16, 20.
12. Nothing due May 11. The last homework was going to be a little project in doing a piece of mathematics but it is too late given the fact that there will be a final exam. To test yourself and see if you have gained in understanding from the course, try to write all this out as clearly as you can after you figure it out.

    Read Rudin Chapter 9, ``The contraction principle'' on your own. Let $F:[0,1]\times\mathbb{R}$ be continuous and Lipschitz continuous in the second variable, meaning that there is a constant $C$ such that

    $$\vert F(x,y)-F(x,z)\vert\le C\vert y-z\vert\ \forall\ x\in[0,1],\ y,z\in\mathbb{R}.$$ (2)

    
    
    Suppose that for some $\delta >0$ $f:[c,c+\delta ]\longrightarrow \mathbb{R}$ is a differentiable function, with $[c,c+\delta ]\subset[0,1],$ satisfying the differential equation

    $$f'(x)=F(x,f(x))\ \forall\ x\in [c,c+\delta ].$$ (3)

    
    
    1. Show that 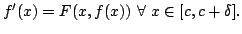$f$ is continuously differentiable on $[c,c+\delta]$ and that it satisfies the integral equation

       $$f(x)=f(c)+\int_c^xF(t,f(t))dt\ \forall\ x\in[c,c+\delta ].$$ (4)

       
       

    2. Conversely show that if $f:[c,c+\delta ]\longrightarrow \mathbb{R}$ is a continuous function which satisfies (4) then it is differentiable and satisfies (3).
    3. Fix some real number $y\in\mathbb{R}$ and show that

       $$S=\{f\in\mathcal{C}([c,c+\delta]);f(c)=y\}\subset\mathcal{C}([c,c+\delta ])$$ (5)

       
       
       is closed with respect to the supremum metric.
    4. For $y\in\mathbb{R}$ and $\delta$ as above show that the map

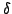       $$I(f)(x)=y+\int_c^xF(t,f(t))dt$$ (6)

       
       
       defines a map from $S$ into $S$ and that this map satisfies

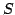       $$d_\infty(I(f),I(g))\le C\delta d_\infty(f,g)$$ (7)

       
       
       where $C$ is the constant in (2).
    5. Conclude that for $\delta >0$ sufficiently small (depending only on $y$ and $F$ but not $c)$ there is a unique differentiable function on $[c,c+\delta]$ satisfying

       $$f'(x)=F(x,f(x))\ \forall\ x\in[c,c+\delta],\ f(c)=y.$$ (8)

       
       

    6. No big hints for the last part! Show that, given $y\in\mathbb{R},$ and under the same conditions as above there is a unque differentiable function on $[0,1]$ satisfying the intial value problem

       $$f'(x)=F(x,f(x))\ \forall\ x\in[0,1],\ f(0)=y.$$ (9)