There are some answers in the postscript and acrobat versions.
This test is closed book, no books, papers or notes are permitted. You may
use theorems, lemmas and propositions from the class and book. Note that
where
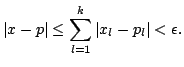 is mentioned below the standard metric is assumed.
is mentioned below the standard metric is assumed.
There are 5 questions on the actual test, I think they are mostly easier
than these ones.
- Consider the function
![$ \alpha :[0,1]\longrightarrow
\mathbb{R}$](img532.png) defined by
defined by
Show carefully, using results from class, that any monotonic increasing
function
![$ f:[0,1]\longrightarrow \mathbb{R}$](img534.png) which is continuous at
which is continuous at
 is Riemann-Stieltjes integrable with respect to
is Riemann-Stieltjes integrable with respect to 
- Let
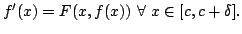 be a continuous function on
be a continuous function on ![$ [a,b].$](img537.png) Explain
whether each of the following statements is always true, with brief but
precise reasoning.
Explain
whether each of the following statements is always true, with brief but
precise reasoning.
- The function
 is well defined.
is well defined.
- The function
 is continuous.
is continuous.
- The function
 is decreasing.
is decreasing.
- The function
 is uniformly continuous.
is uniformly continuous.
- The function
 is differentiable.
is differentiable.
- The derivative
 on
on ![$ [a,b].$](img537.png)
- If
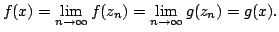 is differntiable and
satisfies
is differntiable and
satisfies


 show that there is a point where
show that there is a point where

- If
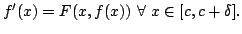 is a strictly positive continuous function on
is a strictly positive continuous function on ![$ [-1,1],$](img545.png) meaning
meaning
![$ \inf_{[-1,1]} f>0,$](img546.png) show that
show that
 is continuous.
is continuous.
- (This is basically Rudin Problem 4.14)
Let
![$ f:[0,1]\longrightarrow [0,1]$](img548.png) be continuous.
be continuous.
- State why the the map
 from
from ![$ [0,1]$](img75.png) to
to
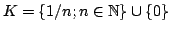 is
continuous.
is
continuous.
- Using this, or otherwise, show that
![$ L=\{x\in[0,1];f(x)\le x\}$](img550.png) is
closed and
is
closed and
![$ \{x\in[0,1];f(x)<x\}$](img551.png) is open.
is open.
- Show that
 is not empty.
is not empty.
- Suppose that
 for all
for all ![$ x\in[0,1]$](img499.png) and conclude that
and conclude that  is open in
is open in ![$ [0,1]$](img75.png) and that
and that
![$ L\not=[0,1].$](img554.png)
- Conclude from this, or otherwise, that there must in fact be a point
![$ x\in[0,1]$](img499.png) such that
such that 
- Consider the function
for
![$ x\in[0,100].$](img557.png)
- Explain why
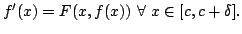 is differentiable.
is differentiable.
- Compute

- Show that there exists
 such that
such that  for
for

- Show that there must exist a point
 with
with  and
and 
Richard B. Melrose
2004-05-18
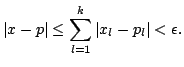 is mentioned below the standard metric is assumed.
is mentioned below the standard metric is assumed.
![$ f:[0,1]\longrightarrow \mathbb{R}$](img534.png) which is continuous at
which is continuous at
![]() be continuous.
be continuous.
![$ x\in[0,100].$](img557.png)