Problem 3

Prove that in any metric space, a finite union of compact subsets is compact.

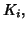
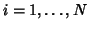
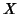
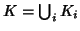
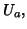
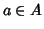
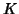
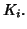
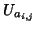
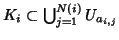
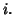
Proof. [Solution] Let $K_i,$ $i=1,\dots,N$ be a finite collection of compact sets in a metric space $X$ and let $K=\bigcup_i K_i$ be their union. 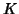An open cover $U_a,$ $a\in A$ of $K$ covers each of the $K_i.$ By the assumed compactness there is a finite subcover $U_{a_{i,j}}$ such that $K_i\subset \bigcup_{j=1}^{N(i)}U_{a_{i,j}}$ for each $i.$ All these sets taken together give a finite subcover of $K$ which is therefore compact. $\qedsymbol$