Applied/Computational Multivariate Statistical Analysis and Random
Matrix Theory
My goal is to devise stable and efficient algorithms for computing the
density, distribution, and quantile functions of select eigenvalues (and
functions thereof) of the classical random matrix ensembles - Wishart,
Jacobi, and Laguerre.
These functions are a fundamental tool in many multivariate
statistical methods, such as hypothesis testing, principal component
analysis, canonical correlation analysis, multivariate analysis of
variance, etc. (Muirhead, 1982). This type of analysis is
an integral
part of many practical applications where multiple signal
sources/receivers are present and thus random covariance matrices
naturally occur. Applications include telecommunications and wireless
networks,
image and signal processing, military applications (automatic 3D
target recognition and classification), etc.
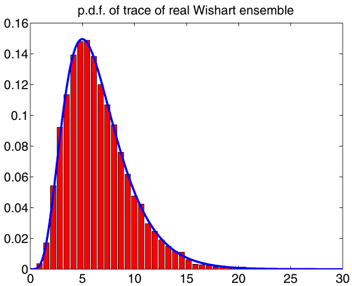
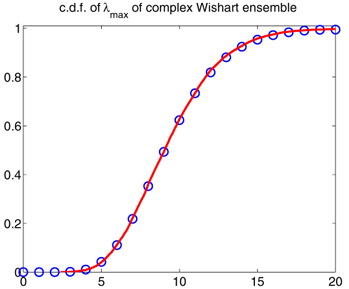
FIGURE: Blue = Analytical, Red = Empirical
LEFT: p.d.f. of the trace
of the 3-by-3 Wishart ensemble with 4 degrees of freedom and covariance
matrix diag(0.25,0.4,1).
RIGHT: c.d.f. of the largest eigenvalue of the 3-by-3 complex
Wishart
ensemble with 4 degrees of freedom and covariance matrix diag(1.1,1.2,1.2).
Many explicit formulas for the distributions of the eigenvalues of the
classical random matrix ensembles have been known for over 40 years
(Constantine 1963, James 1964, Muirhead 1982).
Unfortunately, most of these formulas are in terms of the hypergeometric
function of a matrix argument - an extremely slowly converging series of
Jack functions.
The hypergeometric function of a matrix argument has been incredibly
difficult to compute even in the simplest cases (matrix argument of size
3 or 4); the development of efficient algorithms for its computation has
been identified as a central open research problem in a large number of
recent publications.
(In about 50% of the papers returned by a search at
http://ieeexplore.ieee.org
for "hypergeometric
function" and "matrix argument").
Recently, I developed the first practical algorithm (see also our paper) for computing the hypergeometric
function of a matrix argument. This new algorithm
is very efficient for matrix arguments of size up to 10 (takes at most a
few seconds time) and is exponentially faster than the previous best
algorithm of Gurierrez, Rodriguez and Saez (ETNA, 2000): on the same
5-by-5 example our algorithm takes less than 1/100 of a second as opposed
to 8 days.
Jointly with Ioana Dumitriu, I also established
formulas for the
distributions of the extreme eigenvalues of the Jacobi random matrix
ensemble.
My algorithms for computing the
hypergeometric function of a matrix argument were used to produce the
figures above. It can also be used to observe the convergence of the
largest eigenvalue of a Wishart matrix to the Tracy - Widom limit of order
1, below (see Tracy and Widom, 2000). Such limits apply much more
generally (Soshnikov, 2002).
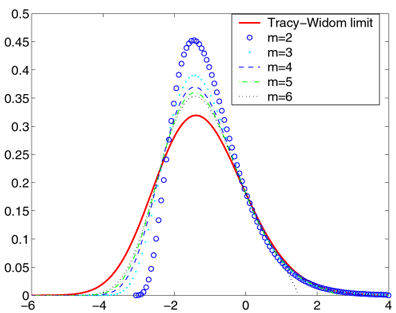
Figure: Convergence of the density of the largest eigenvalue of the m-by-m
Wishart matrix
with 2m degrees of freedom to the Tracy-Widom law of order 1.
References:
-
A. G. Constantine, Some non-central distribution problems in multivariate
analysis, Ann. Math. Statist.
34 (1963), 1270–1285.
-
R. Gutierrez, J. Rodriguez, and A. J. Saez, Approximation of
hypergeometric functions with matricial
argument through their development in series of zonal polynomials,
Electron. Trans. Numer. Anal. 11
(2000), 121–130.
-
Alan T. James, Distributions of matrix variates and latent roots derived
from normal samples, Ann. Math.
Statist. 35 (1964), 475–501.
-
P. Koev, Software for computing the hypergeometric function of a matrix
argument,
available here.
- P. Koev and I. Dumitriu. The distributions of the extreme eigenvalues
of the complex Jacobi random matrix ensemble, submitted to SIMAX,
available here.
-
P. Koev and A. Edelman, The efficient evaluation of the hypergeometric
function of a matrix argument,
Math. Comp.,
75 (2006), 833-846. (PDF).
-
R. J. Muirhead, Aspects of multivariate statistical theory, John Wiley &
Sons Inc., New York, 1982.
-
Alexander Soshnikov, A note on universality of the distribution of the
largest eigenvalues in certain sample
covariance matrices, J. Statist. Phys. 108 (2002), no. 5-6, 1033–1056.
-
Craig A. Tracy and Harold Widom, The distribution of the largest
eigenvalue in the Gaussian ensembles:
beta = 1, 2, 4, Calogero-Moser-Sutherland models (Montreal, QC, 1997),
CRM
Ser. Math. Phys., Springer,
New York, 2000, pp. 461–472.


