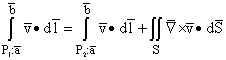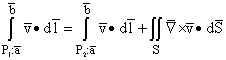Sometimes we want to evaluate a circulation type path integral along  a path on which the evaluation seems difficult, while there is another path with the same endpoints on which the integration would be easy. We can then use Stokes' theorem to relate the difference between the two to a flux integral of the curl of the vector integrand over a region between them. If the vector field of the integrand is conservative, its curl will vanish and the two path integrals will be the same. Even when the field is not conservative, the flux integral involved may be relatively easy.

Examples

Caution

Example