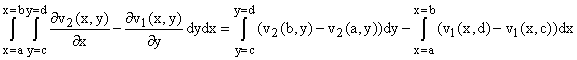
For a rectangle: By the ordinary fundamental theorem of calculus, we have

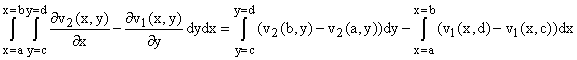
For a right triangle: for convenience we choose a triangle bounded by line x = 0, y = 0 and .
We similarly get:

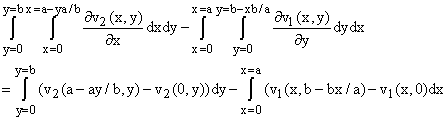
Rearrangement of the right hand side gives the theorem for rectangles and right triangles.
It means that for R a rectangle or right triangle in the x-y plane, (for which dS = dSk) we have

Both sides of this equation are finitely additive: that is, if we take two disjoint regions, and evaluate either one over both, you get the sum of their values on the two regions separately. This is true even if the regions share a common boundary, because the line integrals will cancel out over the common boundary which ceases to be a boundary.
The result follows from additivity for any region that can be broken up into rectangles and triangles, which accounts for most regions we will encounter.