We often encounter curves which represent the orbit or path of a particle or object subject to some environment. If we can deduce the path of the object we obtain formulae for the position of its center of mass, say, as a function of time.We find x(t), y(t) and z(t) and so can write down a position vector for it:  r(t) = x(t)i+y(t)j+z(t)k.
We now ask: what are the interesting properties of this path, and how can we express them, given information of this kind? We assume that the motion of our object is sufficiently smooth that all the functions mentioned so far are differentiable, and their derivatives are differentiable as well.Actually the information contained in the expression for r(t) is of two kinds. It contains the geometric information about the path and its location and shape. It also contains information about how fast the object moves along the path.Given a sufficiently smooth path we can define the following constructs for it:

1. Arclength, s,  along the path P: divide the path up into tiny intervals that each look like straight line segments, and sum the lengths of them all.

3. The tangent vector, t(r), to P at r(t). This is a unit vector in the direction of the tangent line.

4. The curvature,(r) of P at r(t). This is the magnitude of the derivative  of the tangent vector with respect to arc-length along the curve. The curvature has the dimension of an inverse length.

6. The plane of curvature of P at r(t). This is the plane spanned by the tangent vector and its derivative with respect to arclength.

7. The normal vector, n(r) to P at r(t). This is a unit vector  normal to the tangent vector in the plane of curvature, in the direction toward which the curve veers.

8. The center of curvature to P at r(t)  is the point a distance given by the radius of curvature along n from r.

9. The torsion of the P at r(t): this is the magnitude of the derivative of the normal vector n(r) with respect to arclength along the path. This involves third derivatives of r(t), and measures how much the path "twists".

All of these are geometric properties of paths. In addition there is a non-geometric property, the rate of change of arclength with respect to time, or speed of motion along the path, ds/dt.

All of these constructs can be computed in a reasonably straightforward way in terms of derivatives of r(t). It is wise to try to understand what these these properties represent and to realize that they are all easily computable. Memorizing formulae for them is probably a waste of time and effort.
Curves in three dimensional space and hence paths along them can also be described as the intersection of two surfaces, and surfaces can be defined by single equations interrelating x y and z. Thus you sometimes encounter curves that are presented as the set of points obeying two equations. It is interesting to note, that it is quite easy to represent all the geometric constructs above given representation of a curve as the solution set to two equations without parametric representation as described here. We shall see this in a later section.
We now show how to represent these constructs given r(t). (Obviously the parameter used can have any meaning at all and need not represent time, and the discussion will be the same. Since time is the most  common parameter encountered we will use terminology appropriate to it.)

1. By the Pythagorian theorem we have

ds² = dx²+dy²+dz²;

we can immediately compute speed along the curve:

2. The tangent line at r: given a change dt in time on the path we have:

Thus the tangent line to P at (x,y,z) is the line which in parametric form is

3. A tangent vector along the curve is a vector in the direction of this line, such as . The tangent vector t is a unit vector in this direction so we must divide this vector by its magnitude, which is :

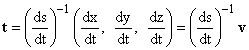
Here v is the velocity vector at r. Thus t is velocity divided by speed.

4. We can compute by the chain rule: computing and remembering that the latter factor is , the reciprocal of the speed. In computing we get terms from differentiating the inverse speed and from differentiating the velocity; the latter gives the acceleration a divided by the speed: .

Note

Here t by definition always has magnitude 1; its derivative must therefore be normal to it.Acceleration in general is not normal to velocity; differentiating the inverse speed produces a multiple of the velocity vector which has the effect of removing the component of acceleration in that direction. Thus has the magnitude of the component of acceleration normal to the velocity, divided by the speed. This can be stated as

We therefore find

6. The plane of curvature is that spanned by a and t.

7. The normal vector n(r) is the unit vector in the direction of (a - (at)t):

8. The center of curvature is the point r.

9. The torsion may be obtained by differentiating n with respect to s, again by the chain rule.

Exercise