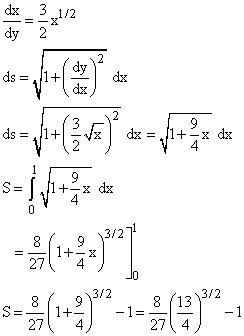To calculate the distance, S, along a curve C between points A and B.

This distance is called arc length of C between A and B.

Let Ds be the distance along the curve between M and N and Dx, Dy their difference in coordinates.

When M and N are very close to each other,

and by the Pythagorean theorem we get

.

We approximate S by a succession of chords, so that the sum of their lengths tends to S as their number increases.

The length S becomes the integral of ds from A to B.

Length S

If the curve C is expressed by parametric equations x(t), y(t):

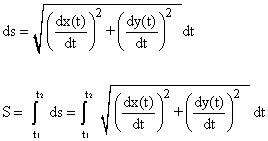
If the curve C is expressed by y = f(x):

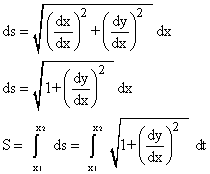
Examples:

Circle

The parametric equations of a circle of radius b are

Calculate the arc length S of the circle.

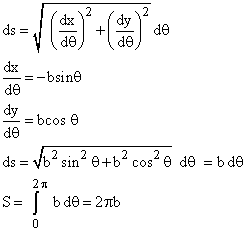
Astroid

The parametric equations of an astroid are

x = cos³t

y = sin³t

Calculate the arc length of 1 / 4 of the astroid (0 t / 2).

Cycloid

A cycloid is the curve traced out by a point on the circumference of a circle when the circle rolls along a straight line in its own plane. The equations of a cycloid created by a circle of radius 1 are

x(t) = t - sin t

y(t) = 1 - cos t

Calculate the arc length S of the cycloid for 0 t / 2.

Ball trajectory

The equations of the trajectory of a thrown ball are

x = at

y = bt - 16t²

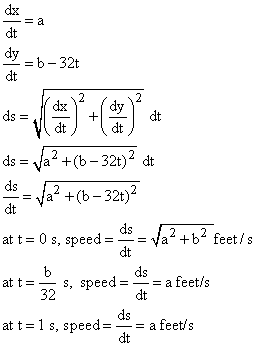
Example 5

Calculate the arc length of y = x² between x = 0 and x = 2.

Example 6

Calculate the arc length of the curve y = x^3/2 between x = 0 and x = 1.

Comment