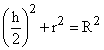
We slice a sphere of radius R by a cylinder of height h and radius R.  

Minimize the surface area of the cylindrical sides if the sphere is fixed.

Condition: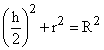

Area of the cylindrical sides: A= 2prh

We minimize

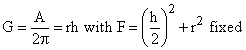
Compure partial derivatives

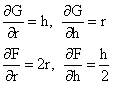
The critcal condition becomes

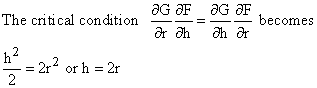
But here it is the condition for maximum cylindric area; the minimum area, zero, occurs at h = 0, r = R and at r = 0, h = 2R.