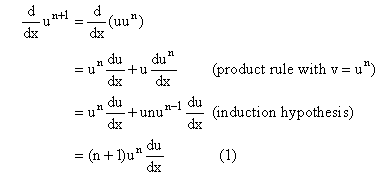
1. Proof of the power rule for n a positive integer.

We prove the relation using induction

1. It is true for n = 0 and n = 1. These are rules 1 and 2 above.

2. We deduce that it holds for n + 1 from its truth at n and the product rule:

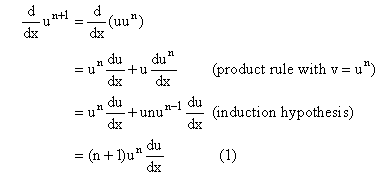
2. Proof of the power rule for all other powers.

Let .

By definition, we have v^q = u^p

Therefore, by implicit differentiation and the integral power rule we have

or

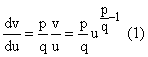
For irrationals we invoke continuity using the fact that (1) holds for all positive rationals and there are rationals that approach any irrational.

For negative powers we can apply the implicit rule to uⁿu^-n = 1.

The desired result follows by the positive power rule and the product rule: