Research Group
- Morris R. Flynn (University of Alberta)
- Aslan R. Kasimov (KAUST)
- Jean-Christophe Nave (McGill University)
- Rodolfo Ruben Rosales (MIT)
- Benjamin Seibold (Temple University)





Support

This material is based upon work supported by the National Science Foundation under Grants No. DMS-1007899 and DMS-1007967, Collaborative Research: Phantom traffic jams, continuum modeling, and connections with detonation wave theory.
Any opinions, findings and conclusions or recomendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation (NSF).
Overview
This web site presents theoretical results about special traveling wave solutions of continuum traffic models. We consider mathematical equations that model traffic similar to the equations of fluid flow. Specifically, we consider the Payne-Whitham model, the Aw-Rascle model, and generalizations thereof. In the simplest case, a single-lane, straight, and uniform road is considered. The models are purely deterministic. All drivers behave according to the same laws, and fully predictably. The considered traffic models predict a nice, uniform traffic flow at low traffic densities. However, above a critical threshold density (that depends on the model parameters) the flow becomes unstable, and small perturbations amplify. This phenomenon is typically addressed as a model for phantom traffic jams, i.e. jams that arise in the absence of any obstacles. The instabilities are observed to grow into traveling waves, which are local peaks of high traffic density, although the average traffic density is still moderate (the highway is not fully congested). Vehicles are forced to brake when they run into such waves. In analogy to other traveling waves, so called solitons, we call such traveling traffic waves jamitons.
Our research is based on the observation that the considered traffic models are similar to the equations that describe detonation waves produced by explosions. Employing the theory of denotation waves, we have developed ways to analytically predict the exact shape and the speed of propagation of jamitons. Numerical simulations of the considered traffic models show that the predicted jamiton solutions are in fact achieved, if the initial traffic density is sufficiently dense. The considered jamitons can qualitatively be found both in observed real traffic as well as in experiments. The theoretical description of the jamiton solution admits a better understanding of their behavior.
Our work also demonstrates that jamitons can serve as an explanation of multi-valued fundamental diagrams of traffic flow that are observed in measurement data. In these, the spread in measurement data is caused by the unsteadiness of jamiton solutions in a systematic and predictable fashion. While the multi-valued nature in real fundamental diagrams is most likely due to a variety of effects, our studies show that traffic waves must not be neglected in the explanation of this phenomenon.
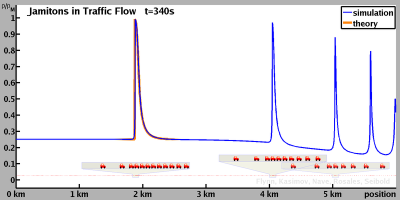
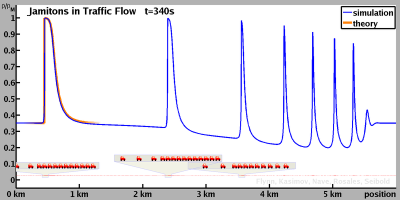
Further findings of our research are trains of multiple jamitons that can occur on long roads. In the language of detonation theory, such traffic roll waves are very similar to roll waves in shallow water flows. Moreover, on long periodic roadways, final states can arise that consist of multiple jamitons. Interestingly, these individual jamitons can be quite different from each other, resulting in highly complex traffic behavior, even after long times of traffic equilibration.
Theoretical Results
We consider continuum two-equation ("second order") traffic models, such as the Payne-Whitham or the Aw-Rascle equations for traffic flow. The traffic flow is not modeled as individual vehicles. Instead, the evolution of a continuous vehicle density function and a continuous velocity function is described. We consider inviscid models, i.e. any smoothing exchange of momentum between neighboring vehicles is neglected. While in reality a small amount of viscosity is obviously present, the inviscid model can be interpreted as a limiting case that admits a simpler analysis. The considered models are purely deterministic, and all drivers behave according to the same laws.
Phantom traffic jams
It is well known that two-equation traffic models are linearly unstable for sufficiently large densities. In other words: A chain of equidistant vehicles that move all with the same velocity will not remain in this nice configuration. Instead, a small perturbation grows, and builds up to become a wave of high vehicle density. This phenomenon is called phantom traffic jam, since it arises in free flowing traffic, without any obvious reason, such as obstacles, bottlenecks, etc. Instabilities in traffic flow and the onset of phantom traffic jams have been studied extensively in various types of traffic models. In continuum traffic models, there are two competing effects. On the one hand there is a stabilizing traffic pressure due to preventive driving. On the other hand, there is a destabilizing effect, which comes from the combination of drivers slowing down when the vehicle density is higher and a delay in the adjustment of drivers to new conditions (the adjustment time is inverse to the "aggressiveness" of the drivers). If the density is above a certain threshold, then the destabilizing effect outweighs the stabilizing pressure, and small perturbations grow.
Jamitons
While the instability that leads to a local concentration of vehicles is understood and reported in many papers, the exact shape of the final traffic jam wave has not been addressed in traffic literature. Our studies show that in inviscid Payne-Whitham type traffic models, instabilities grow into traveling detonation waves. These consist of a sharp jump in vehicle density (a shock) on one side, and a smooth decay in density on the other side. These detonation waves are stable structures that travel unchanged with a constant velocity along the road. In analogy to traveling waves in other fields, solitons, we decided to christen the traveling traffic waves jamitons.
Properties of jamitons
Our analysis is able to predict fundamental properties of such jamitons. A central result is that sharp shocks must always face towards incoming vehicles. Furthermore it can be proved that jamitons always travel slower than the individual vehicles. Hence, vehicles run into a sharp and sudden increase in density (the end of a phantom traffic jam), which forces each vehicle to brake very suddenly. Then, vehicles accelerate again our of the jamiton. Our analysis also shows that jamitons are stable structures. They can only vanish by strong smoothing effects (extremely cautious drivers) or a lowering of density (a widening road, vehicles exiting).
Jamitinos
A growing jamiton may trigger a new instability downstream the road. This instability can also grow and become another traveling wave. A jamiton has given birth to another traffic wave: a jamitino. In a similar fashion, the second traveling wave may trigger a third wave, and so on. Thus, a single instability can trigger an infinitely growing sequence of jamitinos. This phenomenon is visible in the videos below. It resembles roll waves in shallow water flows.
Conclusions for traffic modeling
For simple traffic laws, the shape of jamitons can be described exactly, allowing a precise prediction of the maximum traffic density that is achieved in the presence of instabilities. This result is fundamentally based on the exact shape of the traveling traffic waves, and traditional analysis of continuum traffic models has not been able to make such predictions. Furthermore, having a description of the nonlinear traffic waves allows a study of the traffic outcome in dependence on the model parameters, such as anticipation and aggressiveness of the drivers. While one jamiton does not delay the travel time of individual vehicles significantly (vehicles travel through a jamiton rather quickly), the sharp jump in vehicle density is a potential hot spot for accidents. In addition, the results indicate that jamitons rarely stay alone. In practice, whole trains of jamitons can be expected in long stretches of heavy traffic, resulting in significantly increased fuel consumption, driver aggrevation, wear and tear on materials, and risk for accidents. Consequently, a detailed understanding of the structure of and the interaction between jamitons can be a fundamental step in understanding the mechanics of traffic flow, and thus working towards ameliorating the above effects.
Results for a Circular Road
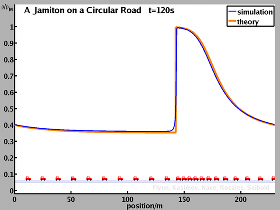
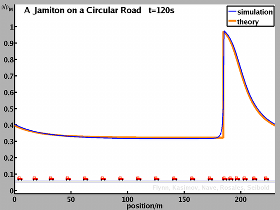
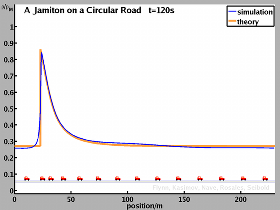
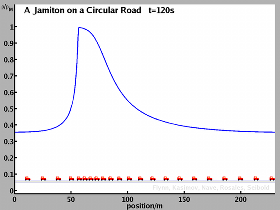
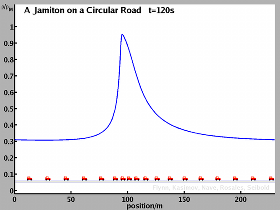
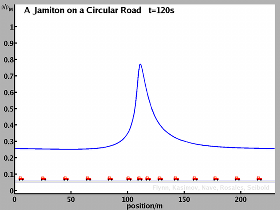
A circular road is a particular friendly case for an analysis, since the total number of vehicles is exactly conserved. If the road is not too long, traffic will in general form one single traveling wave, i.e. a single jamiton, and thus a single shock is observed. Below figures and videos show the results of simulations and theoretical predictions for the case of a circular road of length 230m.
In the case of inviscid equations a sharp shock is realized. Here, the final solution is predicted theoretically. The match between theory and numerical results is generally very good. While the inviscid equations allow a simple analysis, using the Rankine-Hugoniot conditions at the shock, the resulting vehicle behavior is somewhat extreme. Vehicles slow down from high to low velocity in zero time.
Inviscid Model
Large number of vehicles (22)
Download Video side view (divx, 4MB)
Download Video 3D view (divx, 10MB)
Medium number of vehicles (18)
Download Video side view (divx, 4MB)
Download Video 3D view (divx, 10MB)
Small number of vehicles (14)
Download Video side view (divx, 4MB)
Download Video 3D view (divx, 10MB)
In real traffic flow, a small viscosity is present. The physical rationale is that a fast vehicle running towards a slow vehicle results in the fast vehicle slowing down, and (to some extent) the slow vehicle speeding up, before a minimum distance is reached. Unlike above described traffic parameters (adjustment time, preventive driving), the nature of viscosity is difficult to model and extract from real traffic flow. The inviscid equations are expected to be a good approximation to real traffic with a small viscosity.
For comparison, below are simulation results for viscous traffic equations. The general behavior is similar to the inviscid case. In particular, again a traveling wave solution is obtained. However, now with continuous density and velocity functions (the shock is smoothed out). As a result, vehicles brake earlier and more smoothly.
Viscous model
Large number of vehicles (22)
Download Video side view (divx, 4MB)
Download Video 3D view (divx, 10MB)
Medium number of vehicles (18)
Download Video side view (divx, 4MB)
Download Video 3D view (divx, 8MB)
Small number of vehicles (14)
Download Video side view (divx, 4MB)
Download Video 3D view (divx, 8MB)
Comparison with Experimental Results
In March 2008, Sugiyama et al. have published an article Traffic jams without bottlenecks - Experimental evidence for the physical mechanism of the formation of a jam in the New Journal of Physics, in which they report experimental results of traffic waves. On a circular road of 230m length, 22 vehicles were placed equidistantly, and the drivers were instructed to drive, trying to preserve a fixed distance and fixed velocity. As the video below shows, small instabilities amplify, and a traveling arises that moves backwards on the road. Sugiyama et al. conclude: Finally, a jam cluster appears and propagates backward like a solitary wave with the same speed as that of a jam cluster on a highway.
In our simulations, a circular road of 230m length is considered. The desired velocity resembles the velocity in the experiment. A comparison of our computational results for 22 vehicles with the experimental result reveals strong similarities. While there is no one-to-one match in every detail, we do believe that the solitary wave found in the experiment is the same as the jamiton we find analytically and by numerical experiment.
Results for an Infinite Road
Below videos show simulations of a long road with a small initial perturbation. The instability grows into a jamiton. The shape of the jamiton converges to the theoretically predicted shape. In addition, a train of jamitinos is triggered, each of which grows to an independently traveling jamiton.
Comparison with Real Traffic
A nice video of emergent phantom traffic jams (copyright: Dirk Helbing) shows a long straight road in Cairo, Egypt. Strong similarities with the above simulations are present. The typical shape of jamitons is visible, as well as their ability to travel backwards on the road. Unfortunately, too many perturbations (on- and off ramps, interactions between multiple lanes) prevent an unperturbed evolution. In particular, roll waves, as predicted by our simulations, are not clearly visible here. We would love to hear of any observations of traffic roll waves.
Explanation of Multi-Valued Fundamental Diagrams
Our studies show that jamitons have a very specific profile: when plotted in a flow rate vs. density diagram, a jamiton is a straight line segment, whose slope is the travel velocity of the jamiton on the road. As such, jamitons form a two-parameter family of curves. As a first parameter, one can choose the vehicle density at the sonic point. For each such density (if the associated uniform flow is unstable), one obtains a maximum jamiton curve (infinitely long), and a one-parameter family of sub-jamitons, parametrized by their length (or their shock height, respectively).
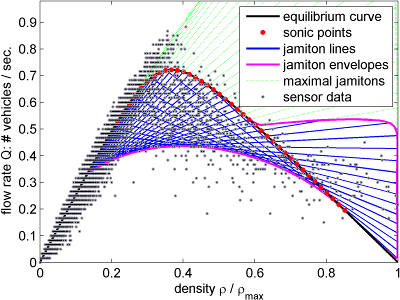
The figure above shows a fundamental diagram, induced by jamitons. The black function is the equilibrium curve that vehicles relax towards. In the regime of densities marked by red dots, uniform traffic flow (of the respective density) is unstable, and jamitons arise. For each red dot (sonic point density), the maximal possible jamiton is marked by a green dotted line segment. Moreover, we calculate how any train of sub-jamitons would appear to a stationary sensor that records flow rate and density in an aggregated fashion (e.g., in intervals of 30 seconds). The resulting averages are given by the blue line segments, and their envelopes by the pink curves. Any point enclosed by the pink curves can arise as a sensor measurement of jamitons states. This construction is placed on top of real sensor measurement data (obtained on the southbound direction of I-35W in Minneapolis, MN; data provided by the Minnesota Department of Transportation). A strong qualitative agreement between the jamiton construction and the data is apparent.
Conclusions
The observation that simple, purely deterministic traffic models possess jamiton solutions indicates that phantom traffic jams are not necessarily caused by individual drivers behaving in a "wrong" way. In fact, they can even occur if all drivers behave by the exact same laws. In the considered traffic models, two key effects work towards the occurrence of phantom traffic jams: first, denser traffic travels slower; and second, it takes a certain "adjustment time" for drivers to react to new traffic conditions. These effects are counter-acted by a certain tendency of the drivers to drive preventively. In light traffic, the good effects dominate. In heavy traffic, the bad effects prevail. Hence, phantom traffic jams are a feature of traffic flow that is not completely avoidable.
Benefits of a better understanding of jamitons
Real traffic possesses jamitons. Hence, a better understanding of their structure can be beneficial for the simulation and prediction of real highway traffic. Furthermore, the research can be one step towards answering the key question "how can the occurrence of phantom traffic jams be avoided". The occurrence of jamitons depends on the model parameters, such as road capacities, speed limits, and driving behavior. A deeper understanding of jamitons may give indications on how to lower peak densities, and how to shift the critical threshold density at which jamitons occur upwards. The latter may be achieved by electronic driving assistence hardware that helps drivers (in a subtle fashion) to accelerate and decelerate more smoothly, and thus to make the occurrence of jamitons less likely.
Press Coverage and Other Links to Our Work
- Traffic jams follow explosive pattern, says researcher (PhysOrg.com, June 5, 2009)
- Mathematicians take aim at 'phantom' traffic jams (MIT news, June 9, 2009)
- Mathematicians Take Aim At 'Phantom' Traffic Jams: New Model Could Help Design Better Roads (ScienceDaily, June 9, 2009)
- Explaining Shadow Traffic Jams with Gas Flows (softpedia.com, June 9, 2009)
- MIT Works to Solve Traffic Jam Problem (DailyTech, June 10, 2009)
- 'Jamitons' slow traffic flow (ft.com, June 11, 2009)
- New Hope for Ending Pointless Traffic Jams (livescience.com, June 12, 2009)
- Math model may decrease phantom traffic jams (msnbc.msn.com, June 12, 2009)
- Mathematicians Take Aim At 'Phantom' Traffic Jams (usnews.com, June 15, 2009)
- Phantom traffic jams (environmentreport.org, June 15, 2009)
- MIT Hopes to Exorcise 'Phantom' Traffic Jams (wired.com, June 17, 2009)
- Catchword jamiton (doubletongued.org, June 17, 2009)
- Study looks to find reason behind phantom jams (wtop.com, June 18, 2009)
- MIT working to eliminate phantom traffic jams (autobloggreen.com, June 18, 2009)
- Mathematically modelling phantom traffic jams (boingboing.net, June 23, 2009)
- Math in the Media: The Year in Science 2009 (ams.org, January 2010)
- Top 100 Stories of 2009: #39: Math - Combined With GPS - Could Fix Traffic Jams (Discover Magazine, January 2010)
- Equation: Factors for Predicting Phantom Traffic Jams (wired.com, June 2010)
- Transport: Signal manoeuvre (Financial Times, August 2010)
- The Ripple Effect of Bad Driving (The New York Times--Opinion, August 2010)
- Keeping Tabs on Traffic (The Wall Street Journal--Blogs, August 2010)
- Holiday Drivers Could Face the "Phantom Traffic Jam" (KYW Newsradio, September 2010)
- Phantom Traffic Jams: It's Your Own Darn Fault (NBC Philadelphia, September 2010)
- A by-the-numbers look at 'phantom' traffic jams (The Philadelphia Inquirer, September 2010)
Scientific Publications
- B. Seibold, M. R. Flynn, A. R. Kasimov, and R. R. Rosales,
Constructing set-valued fundamental diagrams from jamiton
solutions in second order traffic models.
Scientific paper demonstrating that the multi-valued nature of fundamental diagrams of traffic flow (as observed in measurement data) can be explained through the existence of jamitons. - M. R. Flynn, A. R. Kasimov, J.-C. Nave, R. R. Rosales, and B. Seibold.
Self-sustained nonlinear waves in traffic flow.
Physical Review E, 2009; 79 (5)
Scientific paper on the considered traffic models, the prediction of jamitons using the ZND theory of self-sustained detonation waves, and comparisons with computational results. - M. R. Flynn, A. R. Kasimov, J.-C. Nave, R. R. Rosales, and B. Seibold.
On jamitons, self-sustained nonlinear traffic waves.
A brief phenomenological description of the phenomenon of jamitons.
Links
Movies of real-life phantom traffic jams:
- Experimental: Japanese experiment on circular road
- Observation: Video of a emergent phantom traffic jams and jamitons (copyright: Dirk Helbing)