A unified introduction to the theory and practice of modern, near linear-time, numerical methods for large-scale partial-differential and integral equations. Topics include: preconditioned iterative methods; generalized Fast Fourier Transform and other butterfly-based methods; multiresolution approaches including multigrid algorithms, hierarchical low-rank matrix decompositions, and low and high frequency Fast Multipole Methods. Example applications include: aircraft design, cardiovascular system modeling, electronic structure computation, and tomographic imaging.
Grad H subject. Units: 3-0-9. The class is suitable for graduate students from all departments who have affinities with mathematics.
Topics:
Introduction: PDE vs. integral equations, Fourier-based numerical
methods.
Exterior problems:
- Surface integral equations, layer potentials
- The Fast Multipole Method (FMM)
- Partitioned low-rank methods, skeletons, cross-approximation
- Applications to electrostatics, biomolecules, potential flows
Interior problems and variable media:
- Multigrid and relaxation
- Volume integral equations
- Applications to fluid and heat flows, dieletrics, electronic density
High-frequency problems:
- High-frequency FMM
- Butterfly algorithms
- Applications to acoustic and electromagnetic scattering, radar imaging
Prerequisites: Some familiarity with ordinary differential equations, partial differential equations, Fourier transforms, linear algebra, and basic numerical methods for PDE, at the level of 18.085. The assignments will involve computer programming in the language of your choice (Matlab recommended).
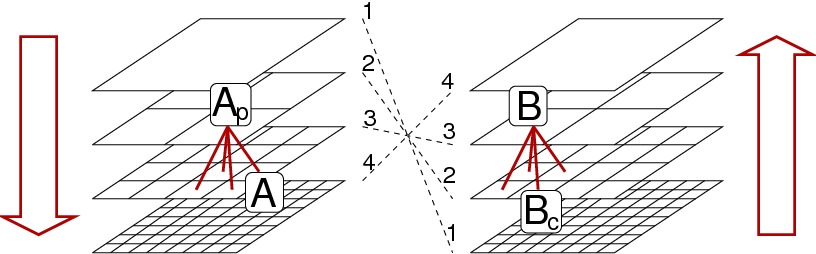
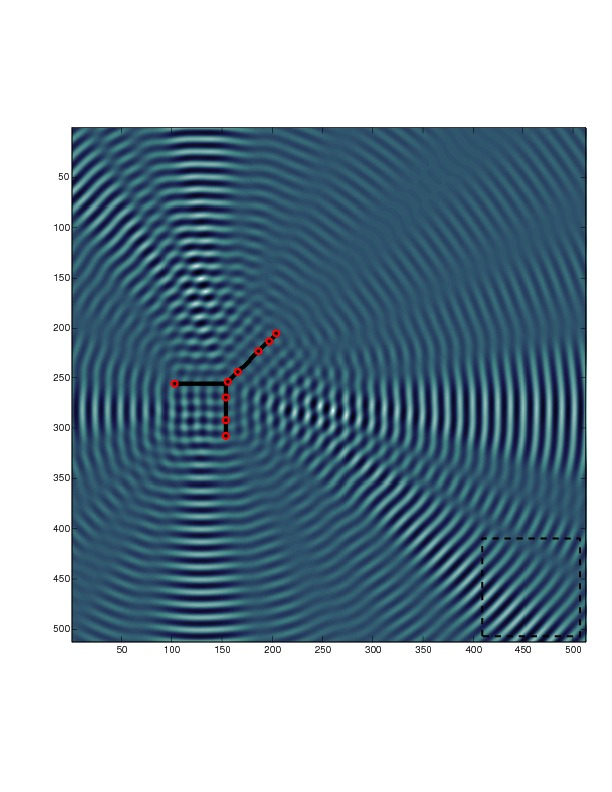
Figures: top-right, the hierarchical tree structure of the butterfly algorithm. Bottom-left, low-rank interactions in the electromagnetic far-field
Here is the current version of the class notes by Laurent Demanet: 04/23/2014
Three references books covering background material on numerical methods for PDE.
- R. LeVeque, Finite difference methods for ordinary and partial differential equations, SIAM, 2007.
- N. Trefethen, Spectral methods in Matlab, SIAM, 2000.
- R. LeVeque, Finite volume methods for hyperbolic problems, Cambridge University Press, 2002.
Date and Time: Tu-Th, 9:30-11:00, room E17-128.
Instructors: Alex Townsend.
TA: TBA
Office hours: Email the instructor.
50% homework, 50% course project.
The homework problem sets will consist of both theoretical problems and numerical experiments. No late copy will be allowed. The lowest score will be dropped. Collaboration is allowed, but the codes and copies you turn in must be original and written by you.
- Problem set 1: (due date October 1st, hand in during class) MRI permittivity model: right-click and download the 257 x 257 dataset, and the 1025 x 1025 dataset. DST code in 1D: dst1.m.
- Problem set 2: (due date November 5th).
- Problem set 3: (due date December 3rd).
The course project will be of a computational or mathematical nature. Each student will have a different project (hopefully tailored to their taste). The project report should be written like a publication: clear and concise. It is a good idea to use LaTeX for the typesetting. Here is a list of possible project topics.
Important dates:
- Choose a project by start of November. Requires consent of the instructor.
- Progress checkup: mid-November (schedule a meeting with the instructor).
- Project presentations: 12/08 and 12/10.
- Project report due: 12/08.
Here are some useful MATLAB scripts:
- CooleyTukey.m: An implementation of FFT when length(input) = 2^k.
- CooleyTukeyRadix3.m: An implementation of FFT when length(input) = 3^k.
- dct1.m: The discrete cosine transform (of type 1).
- dst1.m: The discrete sine transform (of type 1).
- FastPoisson.m: Fast Poisson solver on the square.
- domaindecomposition.m: One-dimensional domain decomposition (schur complement method).
- fastCirculant.m: Fast Circulant matrix-vector product.
- fastToeplitz.m: Fast Toeplitz matrix-vector product.
- fastBlockCirculant.m: Fast matrix-vector product for circulant matrices with circulant blocks.
- diffmat.m: The Chebyshev spectral collocation differentiation matrix.
- chebyshevPoints1.m: Chebyshev points of the 1st kind.
- chebyshevPoints2.m: Chebyshev points of the 2nd kind.
- rectprojmat.m: Rectangular projection matrix.