Suppose M is the matrix that describes T in a given basis B, so that
the columns of M represent the images of the members of B expressed as
linear combinations of the members of B, and M is the matrix similarly
describing T with respect to basis B.
What is the relation of M to M?
Let J be the (Jacobian) matrix whose columns are the basis vectors of
B expressed in terms of those of B.
Then MJ has columns which are the images of the basis vectors of B expressed
in terms of those of B.
To reexpress these in terms of the basis vectors of B you must multiply on the
left by the matrix which expresses the members of B as linear combinations of
those of B.
This is the inverse Jacobian, J-1. We therefore have M
= J-1 MJ, and, by our last result, as claimed:
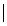 M
M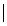 =
=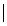 J-1
J-1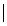
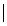 M
M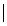
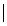 J
J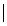 =
= 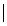 J-1J
J-1J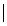
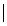 M
M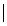 =
=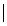 I
I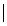
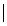 M
M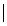 =
= M
M .
.
![]() M
M![]() =
=![]() J-1
J-1![]()
![]() M
M![]()
![]() J
J![]() =
= ![]() J-1J
J-1J![]()
![]() M
M![]() =
=![]() I
I![]()
![]() M
M![]() =
=![]() M
M![]() .
.