|
|
||
|
|
||
|
There are two directions: the r direction is the direction of a vector
from the origin to the point in question;
a unit vector in this direction has representation:
ur = i cos![]() +
j sin
+
j sin![]()
the![]() direction
is normal to this:
direction
is normal to this:
u![]() = -i sin
= -i sin![]() + j cos
+ j cos![]()
The vector r is represented in this coordinate system by r
= rur , where r = (x2+y2)1/2;
since we have
r(t) = x(t) i + y(t) j
we obtain
x = rcos![]() , y = rsin
, y = rsin![]()
Taking derivatives we find
![]()
verify by differentiating yourself that
![]()
which gives:
![]()
![]()
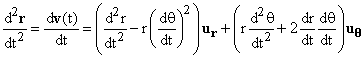
The second and fourth terms here are sometimes referred to in physics as the centrifugal and Coriolis forces. Thus if an object is subject to no external force, so that
![]()
you will find that it obeys
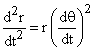 ,
,
and
![]()
The former causes the radial velocity to grow if there is angular motion: the latter slows down the angular motion if the object is moving away from the origin.