Rudin Chapter 4.
- Problem 1.
- The condition
does not imply continuity ofr 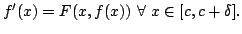 at
at 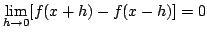 It certainly holds if
It certainly holds if 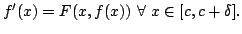 is
continuous, so consider a function which is not continuous at one point,
such as
is
continuous, so consider a function which is not continuous at one point,
such as
Certainly the condition holds for 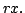 by continuity. For
by continuity. For 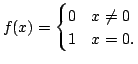 it
also holds, since the definition of limit excludes the value
it
also holds, since the definition of limit excludes the value 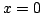 thus
for
thus
for 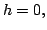
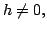
- Problem 4.
- If
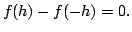 is continuous and
is continuous and
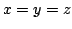 is dense, then for every
is dense, then for every 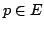 there is a sequence
there is a sequence 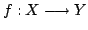 such
that
such
that 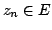 in
in 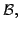 as
as
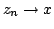 Then, by the continuity of
Then, by the continuity of 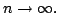
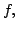 in
in 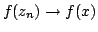 which shows that
which shows that 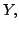 is dense in
is dense in
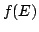 Now, if
Now, if 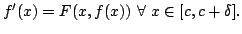 and
and
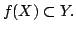 are both continuoues and
are both continuoues and
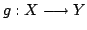 for all
for all 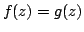 where
where
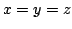 is dense it follows that
is dense it follows that
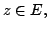 that is
that is 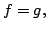 for all
for all 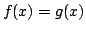 Indeed, by the density of
Indeed, by the density of
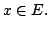 in
in 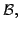 there exists a sequence
there exists a sequence 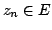 in
in 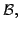 with
with 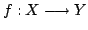 for
all
for
all 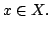 Then
Then
- Problem 15.
- Let
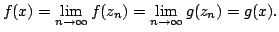 be
continuous and open. Thus if
be
continuous and open. Thus if
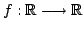 is open then both
is open then both
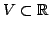 and
and 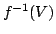 are open. If
are open. If 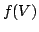 in
in
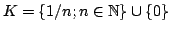 then
then 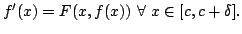 assumes its maximum, and minimum, on
assumes its maximum, and minimum, on ![$ [a,b],$](img434.png) by the continuity
of
by the continuity
of 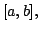 If there is an interior point at which
If there is an interior point at which 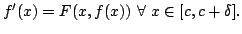 assumes its maximum or
minumum then
assumes its maximum or
minumum then 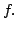 cannot be open, since the maximum, or minimum is
not an interior point of it. Since
cannot be open, since the maximum, or minimum is
not an interior point of it. Since ![$ [a,b]$](img437.png) is connected,
is connected,
![$ f([a,b])=[c,d]$](img438.png) is an interval and
is an interval and
![$ f((a,b))=(c,d)=[c,d]\setminus\{f(a),f(b)\}.$](img439.png) In
particular
In
particular
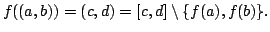 since otherwise these cannot be the
endpoints. Thus
since otherwise these cannot be the
endpoints. Thus 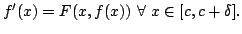 is continuous and injective. Such a map is
necessarily monotonic. To see this explicitly, suppose
is continuous and injective. Such a map is
necessarily monotonic. To see this explicitly, suppose 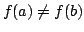 (otherwise replace
(otherwise replace 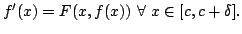 by
by 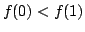 Then if
Then if 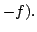
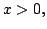 since if not,
since if not,
![$ f([0,x+1])$](img445.png) contains point on both sides of
contains point on both sides of 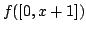
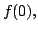 and
and
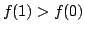 and so would contain
and so would contain 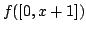 violating the
injetivity. Similarly, if
violating the
injetivity. Similarly, if 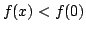 then
then 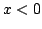 The same argument now
shows that given
The same argument now
shows that given 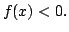
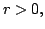 implies
implies 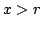 and similarly for
and similarly for
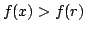 Thus
Thus 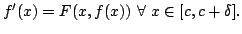 is monotonic.
is monotonic.
Richard B. Melrose
2004-05-18
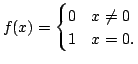 it
also holds, since the definition of limit excludes the value
it
also holds, since the definition of limit excludes the value