Next: Solutions to Homework 6 Up: Solutions Previous: Solutions to Problem set
Chapter 2: Problem 19
Remark It is not in general the case that
![]() and similarly for
and similarly for ![]() Make sure you
understand why!
Make sure you
understand why!
d)
If ![]() is connected and contains at least two points,
is connected and contains at least two points, ![]() and
and
![]() then
then
![]() For any
For any
![]() there must exist at
least one point in
there must exist at
least one point in ![]() with
with
![]() Indeed if not, then
Indeed if not, then
![]() is empty and
is empty and ![]() with
with ![]() and
and ![]() as
above. Since these sets are separated and
as
above. Since these sets are separated and ![]()
![]() shows that
neither is empty this would contradict the connectedness of
shows that
neither is empty this would contradict the connectedness of ![]()
Chapter 2: Problem 20
Suppose
![]() is connected and consider
is connected and consider
![]() where
where
![]() and
and
![]() Then
Then
![]() and
and
![]()
![]() so
so ![]() and
and ![]() are separated. Thus one must
be empty by the connectedness of
are separated. Thus one must
be empty by the connectedness of ![]() changing names if necessary we can
assume that it is
changing names if necessary we can
assume that it is ![]() so
so
![]() must consist only of limit points of
must consist only of limit points of
![]() and necessarily
and necessarily
![]() but then
but then
![]() so
so
![]() and
and ![]() is indeed connected.
is indeed connected.
On the other hand the interior of a connected set need not be
connected. Take the region
![]() This is the union
of the closed first and third quadrants. From the problem below, the two
quadrants are themselves connected. Let us show that the union of two
connected sets with non-empty intersection is connected. Thus suppose
This is the union
of the closed first and third quadrants. From the problem below, the two
quadrants are themselves connected. Let us show that the union of two
connected sets with non-empty intersection is connected. Thus suppose
![]()
![]() are connected sets and
are connected sets and
![]() Then
if
Then
if
![]() with
with ![]() and
and ![]() separted it follows that
separted it follows that
![]() with
with
![]()
![]() Furthermore,
Furthermore, ![]() and
and ![]() are separted for
are separted for ![]() (and the same
(and the same ![]() since
since
![]() and
and
![]() From the
connectedness of
From the
connectedness of ![]() we must have one of
we must have one of
![]() or
or
![]() and one of
and one of
![]() or
or
![]() Of course it
we have both
Of course it
we have both ![]() empty then
empty then
![]() and similarly for the
and similarly for the
![]() 's. So, if necessary swithching
's. So, if necessary swithching ![]() and
and ![]() the only danger is that
the only danger is that
![]() and
and
![]() but then
but then ![]() and
and ![]() but then
but then
![]() contradicting the
assumption. Thus
contradicting the
assumption. Thus
![]() is connected and in particular ths applies
to our union of two quadrants.
is connected and in particular ths applies
to our union of two quadrants.
The interior is the union of the two open quadrants and these are separated, since the closure of each is the corresponding closed quadrant so the union is not connected.
Chapter 2: Problem 21
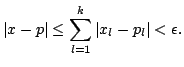 is connected.
is connected.
Chapter 2: Problem 24
Remark: Note that separable and separated are rather unrelated concepts.
We assume that ![]() is a metric space in which every infinite subset has a
limit point (sequentially compact is what I called these in lecture). We
are to show that
is a metric space in which every infinite subset has a
limit point (sequentially compact is what I called these in lecture). We
are to show that ![]() is separable. For each
is separable. For each ![]() choose successively points
choose successively points
![]() for
for
![]() such that
such that
![]() for
for ![]() Either at some point no further choice is possible, or else we can choose
this way an infinite set
Either at some point no further choice is possible, or else we can choose
this way an infinite set
![]() with
with
![]() for all
for all ![]() distinct. By assumption on
distinct. By assumption on ![]() this set
this set ![]() must have a limit point, call
it
must have a limit point, call
it ![]() Since
Since
![]() must be infinte, it must
contain at least two distinct points
must be infinte, it must
contain at least two distinct points ![]() which have
which have
Chapter 2: Problem 26
Suppose ![]() is sequentially compact in the sense that every infinte subset
of
is sequentially compact in the sense that every infinte subset
of ![]() has a limit point. We already know from Exercises 23 and 24 that
has a limit point. We already know from Exercises 23 and 24 that ![]() has a countable basis of open sets. That is, there is a countable
collection of open sets
has a countable basis of open sets. That is, there is a countable
collection of open sets
![]() such that any open set is a union of
elements of
such that any open set is a union of
elements of
![]() That is, given
That is, given
![]() open define
open define
![]() then
then
![]() Suppose
Suppose
Now, replace ![]() by a labelling by integers, so we can write
by a labelling by integers, so we can write
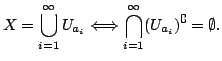
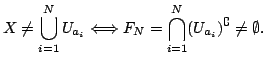 form a decreasing sequence of closed subsets of
form a decreasing sequence of closed subsets of 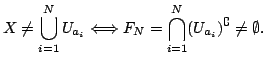 for arbitrarily large
for arbitrarily large 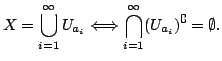 hence in all the
hence in all the 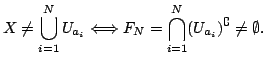 since they are decreasing. In the second case
since they are decreasing. In the second case 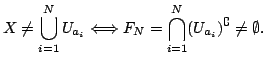 (since they are closed). In either case this gives a point in
(since they are closed). In either case this gives a point in
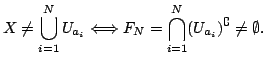 must be empty from some point onwards, giving
us a finite subcover.
must be empty from some point onwards, giving
us a finite subcover.
Remark: In lecture I did not go through the step of
extracting the countable subcover, just used the cover given by ![]() directly.
directly.
Chapter 2: Problem 29
Suppose
![]() is open. Since
is open. Since
![]() is separable, it
contains a countable dense subset, for instance
is separable, it
contains a countable dense subset, for instance
![]() Take a
surjection
Take a
surjection
![]() and write
and write ![]() for
the image of
for
the image of ![]() Since
Since ![]() is open if
is open if ![]() then
then
![]() for some
for some ![]() must contain at least one of the
must contain at least one of the ![]() Consider successively each of the
Consider successively each of the ![]() Again, there is an interval
Again, there is an interval
![]() Now, if
Now, if
![]() consider
consider
Richard B. Melrose 2004-05-18