|
|
|
15.2 Systems of Inhomogeneous Equations
|
|
Discussion: Given a system of inhomogeneous equations(equations
having a non-zero constant term), here are four examples:
| A. |
B. |
2 x + 3 y + 7 z = 2
x - y - z =
1
x +
z = 1
|
x - y - z = 1
x + z = 1
|
| C. |
D. |
x - y = 1
2 x - 2 y = 2
|
x - y = 1
2 x - 2 y = 1
|
A standard problem is to solve them; which means to reduce them to explicit
expressions for x, y and z.
This is feasible in example A; but not in any of the others, for the simple
reason that there is not a unique solution for the others.
With no equations, x, y and z can be chosen freely to represent any point in
three dimensional space. One linear equation can permit you to solve for one
of the three variables in terms of the other two. The space of possible solutions
is reduced one dimension by one equation, to a plane. A second equation can
allow you to solve for a second variable in terms of the third, reducing the
solution space to a line. With two equations that third variable can still be
chosen freely, upon which the other two are determined; there is not one unique
solution to the two equations, but at best a whole line of them.
In general, if there are n variables, you need n linear equations to determine
them all uniquely; but not any n equations will do.
In example B we have 3 variables and only two equations; obviously not enough
to determine a solution.
In cases C and D we have two equations in two variables, but they have the same
content in C and contradictory content in D. There is essentially only one equation
in case C; and case D is self contradictory.
This leads to the following three basic questions
1. When are n inhomogeneous linear equations in n variables uniquely solvable?
2. How do you go about solving them?
3. What can you do when they are not uniquely solvable?
Unique Solvability
Discussion:
A single linear equation, a x + b y + c z = d, can be written as r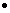 v
= d where r is the vector (x, y, z) and v is (a, b, c).
v
= d where r is the vector (x, y, z) and v is (a, b, c).
Given v, this equation determines the component of r in the direction
of v.
A second equation, say, r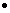 w
= e, determines the component of r in the direction of w.
w
= e, determines the component of r in the direction of w.
As long as v and w have different directions this is new information.
The resulting information is enough, by linearity of the dot product, to determine
the component of r in any direction that lies in the plane of v
and w. (Thus if q = 5 v + 3 w, then r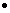 q
= 5 r
q
= 5 r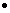 v
+ 3 r
v
+ 3 r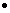 w).
w).
In order that a third vector,t determine new information, it is necessary
(and sufficient). that v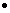 w
and t not lie in the same plane. This is exactly the condition that the
volume of the parallelopiped with edges t, v and w is not
zero; this is the condition that the determinant formed by taking their components
as the rows, does not vanish, since the magnitude of the determinant is this
volume. The same reasoning and the same conclusion apply in any higher dimensional
space.
w
and t not lie in the same plane. This is exactly the condition that the
volume of the parallelopiped with edges t, v and w is not
zero; this is the condition that the determinant formed by taking their components
as the rows, does not vanish, since the magnitude of the determinant is this
volume. The same reasoning and the same conclusion apply in any higher dimensional
space.
Form the square array defined by the coefficients of x, y and z in the three
equations: (or in general n equations in n variables). If the determinant of
this array or matrix is non-zero, the equations determine a unique solution.
Example