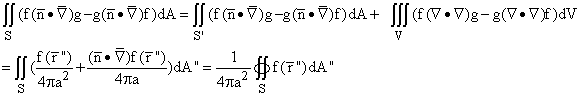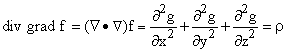|
|
|
14.1 Application of the Divergence Theorem: Laplace's Equation
|
|
The combination div grad , (
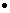
 )
or
)
or  is called the "Laplacian" differential operator,
is called the "Laplacian" differential operator,
The equation (
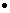
 )
f = 0 is called Laplace's equation. Static electric and steady state
magnetic fields obey this equation where there are no charges or current.
)
f = 0 is called Laplace's equation. Static electric and steady state
magnetic fields obey this equation where there are no charges or current.
Any solution to this equation in R has the property that its value at the
center of a sphere within R is the average of its value on the sphere's surface.
If g(r) obeys Laplace's equation inside a spherical surface, S, of radius
a, centered at r', we have
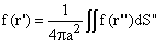
Laplace's Equation
Thus solutions to Laplace's equation are very smooth: they have no bumps
maxima or minima in R and essentially "interpolate" smoothly between
their values on the boundaries of R. We prove this important fact as an application
of the divergence theorem.
This result also implies that if we know the divergence of a vector v and its
curl everywhere, these are differentiable everywhere, and v vanishes
at infinity, then v is uniquely determined. proof box( if there were
two solutions v and v' with the same divergence and curl, then
on applying the double cross product identity we find that every component of
their difference obeys Laplace's equation everywhere. Its value anywhere is
then its average value on a huge circle at infinity, which is 0 by assumption.
The same conclusion holds if v and v' are required to behave at
infinity in the same way, so that v - v' must approach 0 for large
arguments.)
Proof
Suppose our function, f(r), obeys Laplace's equation within some sphere
S centered at r':
div grad f = (
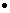
 )
f = 0 inside S
)
f = 0 inside S
We apply the divergence theorem to the vector f g
- g
g
- g f
in the sphere with surface S excluding a tiny sphere of radius b with surface
S' having the same center. We obtain
f
in the sphere with surface S excluding a tiny sphere of radius b with surface
S' having the same center. We obtain
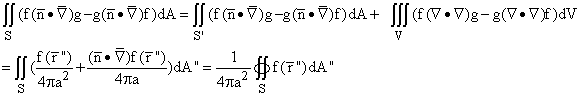
the latter being obtained by substituting for g. The second integral on the
second line vanishes here as can be seen by applying the divergence theorem
again within S and noticing that the Laplacian applied to f is 0.
The right hand side here is the average value of f on S. The similar integral
over S' is evaluated in exactly the same way and is the average value of f on
S'. We conclude that the average value of v on any sphere with center at r'
is the same. Obviously as the sphere approaches radius 0 that average value
becomes the value of f at r'.
The method used in this argument is a very important and general one that is
used in dealing with many differential equations. In fact the use of the divergence
theorem in the form used above is often called "Green's Theorem."
And the function g defined above is called a "Green's function" for
Laplaces's equation.
We can use this function g to find a vector field v that vanishes at
infinity obeying div v = 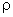 ,
curl v = 0. (we assume that r is sufficently well behaved, integrable,
vanishes at infinity etc...) Suppose we write v as grad f.
,
curl v = 0. (we assume that r is sufficently well behaved, integrable,
vanishes at infinity etc...) Suppose we write v as grad f.
We get
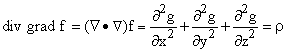
(This equation is called Poisson's equation and is obeyed by the potential
produced by a charge distribution with charge density 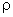 .)
.)
A solution that vanishes at infinity is then given by
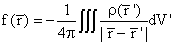
Proof
The same approach can be used to obtain a vector potential A and determine
a vector v obeying

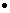 v
= 0, v
v
= 0, v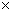
 =
j
=
j
With v =
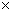 A
we obtain
A
we obtain
(
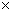 (
(
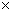 A))
= j
A))
= j
and with the double cross identity
(
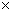 (
(
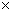 A))
=
A))
=  (
(
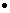 A)
- (
A)
- (
 )
A
)
A
and the "gauge" condition (which we are free to assume) ) 
 A
= 0, we find that each component of A obeys Poisson's equation with
source - the corresponding component of j.
A
= 0, we find that each component of A obeys Poisson's equation with
source - the corresponding component of j.
We may therefore find a formula for each coordinate of A exactly like
the corresponding formula for the scalar potential V. Again v may be
recovered from A by differentiating.
These results are of some use in the study of electromagnetic fields but they
don't solve all problems. Often the known charges and currents induce unknown
charges and currents in conducting surfaces, and one wants to determine the
fields, in circumstances in which there are some unknown charges and /or currents
and you know conditions on the field at the conductor surfaces instead of the
charges and currents in them.
Exercises
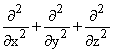 is called the "Laplacian" differential operator,
is called the "Laplacian" differential operator,