Faraday observed that changing magnetic fields produced modifications to the laws of electrostatics: in particular, changing magnetic fields lead to non-conservative electric fields, in which the circulation integral of electric field around a closed path P does not always vanish. In fact his laws describe precisely what such integrals are: a constant multiple of the rate of change of magnetic field flux on any surface bounded by P.

His law is:

Stokes' Theorem for E is

Combining these two equations yields for any surface S:

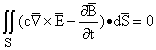
from which physicists conclude:

cE - (B / t) = 0

as the differential form of Faraday's Law.

For convenience, we have chosen units for E and B such the constants c apearing in Ampere's Law and Faraday's Law are the same.