In any coordinate system, in computing an integral over a volume, you break the volume up into little pieces, and sum the value of the integrand at a point in each piece, times the volume of the piece.
In order to do this using a coordinate system w₁ , w₂ , w₃ ,  instead of x, y and z, you must know how much volume is associated with a little box whose boundaries are 6 surfaces, two of which have each w_i fixed, the two separated, in value of this variable, by dw_i .
With the coordinates x,y and z, the region defined in this way is a small rectangular box with volume dxdydz. If the coordinates, w₁ , w₂ , w₃ , are orthogonal,  and ds² = u₁²dw₁² + u₂²dw₂² + u₃²dw₃², then the volume is u₁ u₂ u₃ dw₁ dw₂ dw₃.
In doing integrals it is sometimes convenient to change variables to arbitrary coordinates which are not orthogonal.

What then is the volume?
Making a change of dwi in the variable wi produces a change in each of x, y and z and we can compute these changes. Thus we can compute the vector in x, y, z space that corresponds to this change:
since 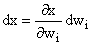, with similar formulae for dy and dz, the change dwi produces a vector change in r of _.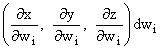
The volume we want is the volume in the small parallelopiped determined by these vectors. But we know the volume in a parallelopiped determined by three vectors: it is the magnitude of the determinant having them as rows.

Explicitly we find that

 dV = dx dy dz = Jdw₁dw₂dw₃ where J is called the Jacobian of the transformation from variables x, y, z, to w₁ , w₂ , w₃ , and is given by

The Jacobian tells you how to express the volume element dxdydz in the new coordinates. If you were to go backward, starting from coordinates w₁ , w₂ , w₃ , and changing to x,y and z, the roles of the two sets would be reversed, and the w's would be differentiated with respect to x y and z in the backward Jacobian J_b, which obeys J_b dx dy dz = dw₁dw₂dw₃.  This implies that J_bis the reciprocal of J: J_b = J^-1.

This last fact can be very useful. Sometimes you know how to express the w's in terms of the x's and not vice versa; you can then compute J_b and determine J to be its reciprocal.

The Jacobian tells us how, in changing variables from any given set of variables of integration to any other to express the volume element in for the old variables in terms of the volume element for the new set.
The same argument works in any dimension. Thus for two variables you get dxdy = J dw₁dw₂ , with J, the Jacobian being the magnitude of the two by two determinant,given by the top left corner of the three by three Jacobian. In four or more dimensions, everything works similalry except the determinant has more and longer rows.

Exercises

Reversing the Order of Integration:

When you are doing several integrals sequentially it may happen that the limits of integration of one integral involve the variable integrated over subsequently. Sometimes, further, you may be able to perform the integrations if you can reverse the order of doing them.
You must be very careful when you change the order of integration under these circumstances: You should draw a picture of the region of integration, and make sure that the limits you deduce for the reverse order correspons to the same region of that picture

Here is a simple example.
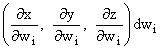