|
|
||
|
|
||
|
If a vector field v is a gradient field (is conservative), how can you find
a function f such that grad f =v?
First Method:
Knowing derivatives of f of course determines f only up to a constant. Thus f(a) can be anything. Once we define path integrals, we can define f(r) anywhere else in R by the equation:
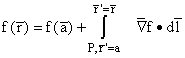
where the path P lies entirely in R. You may choose P to make the computation as easy as it can be.
Second Method:
Another way to compute f is first to fix y and z: whereupon by integrating over x we obtain
![]()
then determine the first term on the right by repeating the procedure with x = x0,, integrating over y:
![]()
and once more, this time integrating over z, to determine the first term here:
![]()
(When using this approach it is very easy to err by counting the same term twice; always check your answer by differentiating it to make sure its gradient is what you started with.).
Third Method:
Perhaps the easiest approach, which works very well on functions you encounter
in texts and in courses and in particular on exams, is to guess the answer,
check by differentiating and improve your guess until it is correct.
The problem here is integrating, and you have some intuition as to how to integrate:
thus you know something about how to integrate polynomials powers exponents,
trigonometric functions and even general rational functions. Here you have
two or three clues: you have derivatives of the function sought with respect
to two or three different variables; this makes the quest for a solution easier
rather than harder, in many cases.
Always try to guess first; always check your answer by differentiating back.
Later on we will describe still another way to find a potential f for v that
is the easiest of all, given that R is all of space, and and you want the potential
to approach a constant value at infinity.