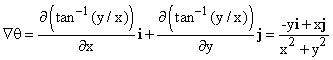
|
|
||
|
|
||
|
Consider its gradient, which is a vector field:
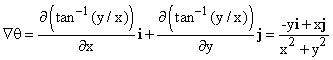
This vector field has cross partials equal at all points except at x = y =0,
where these derivatives don't exist. It is in general not the gradient of a
function. It is the gradient of ![]() which is not a function. However
which is not a function. However![]() is
a well defined function in any simply connected region of 3-space which does
not meet the line r = 0.
is
a well defined function in any simply connected region of 3-space which does
not meet the line r = 0.
Thus ![]()
![]() is conservative in any such region. The seemingly confusing fact that vector
fields can be conservative in one region and not so in another simply reflects
the properties of objects like the angle
is conservative in any such region. The seemingly confusing fact that vector
fields can be conservative in one region and not so in another simply reflects
the properties of objects like the angle ![]() which is a true single valued function only when restricted to be so; confining
its range is one way to keep it single valued.
which is a true single valued function only when restricted to be so; confining
its range is one way to keep it single valued.