The vector whose x,y and z components are the respective partial derivatives of f at (x, y, z), is called the gradient of f, and is written either as grad f  orf. Hererepresents the "differential operator" vector,

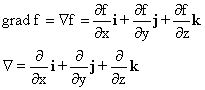
The gradient vector points normal to the tangent plane of  f in two dimensions, and normal  to the tangent hyperplane in higher dimensions. Since it is easily computed, the tangent hyperplane is easily found as well.
Suppose now that f is a differentiable function at (x, y, z) and we want to find its directional derivative on a line L(d) having unit vector d pointing along it. We can always write d as the sum of its projection into the tangent plane of f at (x, y, z) and its projection normal to that plane. f experiences no change at all if we move an infinitesimal distance from (x, y, z) in the tangent plane. Only the component of d normal to the tangent plane, and hence in the direction of the gradient, produces change in f. The directional derivative of f in the d direction is therefore given by the magnitude of the gradient of f there, times the component of n normal to the tangent plane: in other words, by dgrad f, that is, by df.

The gradient therefore gives us a quick way to compute directional derivatives.

The Fundamental Theorem of Calculus on L(d):

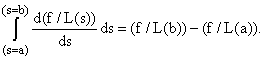
or with dl = dds,