Curvature: Motion in several dimension has two aspects: one is its speed of motion; the other the shape of the curve it follows. The former is measured by the speed of motion, ds/dt, where s = (rr)^1/2.
The latter is measured at each point by the curvature,, of the curve traced. This is the magnitude of the rate of change of a unit vector in the direction of motion with distance s along the curve. Its dimension is that of an inverse length, and its reciprocal 1/, is called the radius of curvature.

The curvature is proportional to the component of the acceleration normal to the velocity with a proportionality constant that can only depend on the speed:

The dimension of av is L²/T³ which implies 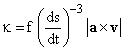up to a constant which constant is 1.

The plane of motion is that normal to av. The torsion of the curve is the magnitude of the rate of change of a unit vector in the direction of av with distance along the curve. There is a formula for it that you might remember exists but should not remember in detail.